1 Préparation des données

1. Ouvrez le fichier d’expression des gènes en utilisant la commande read.table(). Stockez ce data.frame dans l’objet BIC.expr. Vérifiez la taille du data.frame généré en utilisant la commande dim().

data.folder<-"../../projects/du_bii_2019/data/module3/seance4/BIC/"

BIC.expr.file <- file.path(data.folder, "BIC_log2-norm-counts_edgeR_DEG_top_1000.tsv.gz")
BIC.expr <- read.table(file = BIC.expr.file, header = TRUE)
dim(BIC.expr)

[1] 1000  819

2. Ouvrez le fichier qui contient les étiquettes des échantillons en utilisant la commande read.table(). Stockez ce data.frame dans l’objet BIC.sample.classes.

BIC.sample.classes <- read.table(file.path(data.folder, "BIC_sample-classes.tsv.gz"),header = TRUE)

• Vérifiez le nombre d’échantillons disponibles dans ce jeu de données.

dim(BIC.sample.classes)

[1] 819   4

• Déterminez le type de variables disponibles dans ce jeu de données en utilisant la fonction summary().

summary(BIC.sample.classes)

       cancer.type        ER1            PR1            Her2    
 Basal.like  :131   Negative:184   Negative:267   Negative:631  
 HER2pos     : 41   Positive:635   Positive:552   Positive:188  
 Luminal.A   :422                                               
 Luminal.B   :118                                               
 Unclassified:107                                               

La première colonne du data.frame BIC.sample.classes renseigne sur le type de cancer de chaque échantillon. Comme vous pouvez le voir, il y a 5 types de cancer, dont un type qui est Unclassified. Lors de la prédiction du type de cancer, ce type risque de biaiser les résultats. Vous allez supprimer ces échantillons des jeux de données.
A la fin du TP, vous utiliserez les modèles statistiques construits pour prédire le type de cancer de ces échantillons de type “Unclassified”.

3. Supprimez les échantillons correspondant au type Unclassified dans les deux data.frames.

• En utilisant la fonction which(), identifiez les lignes du data.frame BIC.sample.classes qui correspondent au type Unclassified. Vérifiez que vous avez bien sélectionné 107 individus.

ind.uncl <- which(BIC.sample.classes[,"cancer.type"]=="Unclassified")
length(ind.uncl)

[1] 107

• Supprimez ces individus dans le data.frame BIC.sample.classes en utilisant l’indexation négative. Vérifiez la taille du nouveau data.frame. Le nouveau data.frame se nommera BIC.sample.classes.4.

BIC.sample.classes.4 <- BIC.sample.classes[-ind.uncl,]
dim(BIC.sample.classes.4)

[1] 712   4

• Supprimez les échantillons correspondant au type Unclassified du data.frame BIC.expr. Attention, dans le data.frame BIC.expr les échantillons sont présentés en colonnes.

BIC.expr.4 <- BIC.expr[, -ind.uncl] 
dim(BIC.expr.4)

[1] 1000  712

• Pour construire les premiers modèles, vous n’allez pas utiliser les quatre types de cancers, mais seulement deux :
  • Luminal.A,
    
  • non Luminal.A : qui correspondent aux autres types. Vous allez donc transformer la colonne cancer.type du data.frame BIC.sample.classes.2 en une variable qualitative à deux classes : “Luminal.A” ou “no.Luminal.A”.

1. Créez le vecteur new.type qui contient 712 fois (nrow(BIC.sample.classes.2)) la valeur “Luminal.A”.

new.type <- rep("Luminal.A", length = nrow(BIC.sample.classes.4))

2. Identifiez les individus qui ne contiennent pas “Luminal.A” dans la première colonne (colonne cancer.type) du data.frame BIC.sample.classes.4.

ind.noLA <- which(BIC.sample.classes.4[,"cancer.type"]!="Luminal.A")

3. Pour ces individus, assignez la valeur “no.Luminal.A” au vecteur new.type.

new.type[ind.noLA] = "no.Luminal.A"

4. Remplacez la colonne cancer.type du data.frame BIC.sample.classes.2 par le vecteur new.type que vous aurez transformé en facteur (fonction as.factor())

BIC.sample.classes.2 <- BIC.sample.classes.4
BIC.sample.classes.2[,"cancer.type"] = as.factor(new.type)

4. Suppression des variables corrélées

Une des étapes du nettoyage du jeu de données correspond à supprimer les variables (ici les gènes) corrélées. Pour cela, vous allez utiliser la fonction findCorrelation() de la librairie caret. Cette fonction prend en entrée la matrice de corrélation entre les variables et le seuil de corrélation à partir duquel on considère que deux variables sont corrélées.

• Calculez la matrice de corrélation entre les gènes différentiellement exprimés. Comme dans le data.frame BIC.expr.4 les gènes sont en lignes, pensez à transposer votre data.frame.

mat.cor <- cor(t(BIC.expr.4))

• Identifiez les gènes à supprimer en utilisant un seuil de corrléation de 0.8 et la fonction findCorrelation(). Combien de gènes allez vous supprimer.

library(caret)
var.supp = findCorrelation(mat.cor, cutoff = 0.8)
length(var.supp)

[1] 36

• Supprimez ces gènes du data.frame BIC.expr.4.

BIC.expr.4 <- BIC.expr.4[-var.supp,]
dim(BIC.expr.4)

[1] 964 712

5. Pour créer les modèles de prédiction, il est nécessaire d’avoir un data.frame qui regroupe pour chaque échantillon les gènes et son type de cancer.

• Créez le data.frame df.data qui contient :
  • en lignes ; les échantillons
    
  • en colonnes : les gènes et le type de cancer.
    Pour cela, utilisez la commande data.frame().
    
  • La première colonne de votre data.frame df.data doit correspondre aux types de cancer.
    
  • les colonnes 2 à 965 doivent correspondre aux gènes.

df.data <- data.frame(BIC.sample.classes.2[,1], t(BIC.expr.4))

• Assignez “cancer.type” comme nom de colonne à la première colonne de df.data.

colnames(df.data)[1] <- "cancer.type"

2 Préparation des échantillons d’apprentissage et de test

• L’échantillon d’apprentissage est l’échantillon qui va permettre d’apprendre les modèles. Il sera constitué de 2/3 des échantillons sélectionnés de manière aléatoire.
  
• L’échantillon de test est l’échantillon qui va permettre d’estimer les performances non biaisées des modèles. Il sera constitué du 1/3 des échantillons restant.

1. En utilisant la fonction sample() créez un vecteur qui contient le numéro d’indice de 2/3 des individus choisis aléatoirement. Ces individus vont constituter les individus du jeu d’apprentissage.

ind.app <- sample(1:nrow(df.data), size=2/3*nrow(df.data))

2. Créez le data.frame mat.app qui contient les valeurs d’expression des gènes et le type de cancer pour les individus choisis aléatoirement. Cette matrice correspond au jeu d’apprentissage.

mat.app <- df.data[ind.app,]
dim(mat.app)

[1] 474 965

3. Créez le data.frame mat.test qui contient les valeurs d’expression de gènes et le type de cancer pour les individus restants (1/3). Cette matrice correspond au jeu test.

mat.test <- df.data[-ind.app,]
dim(mat.test)

[1] 238 965

3 Validation des deux échantillons.

1. Calculez une analyse en composantes principale en utilisant le data.frame df.data. Pour cela, utilisez la fonction PCA() de la librairie FactoMineR. Pensez à ne pas prendre en compte la colonne renseignant sur le type de cancer car ce n’est pas une variable quantitative.

library(FactoMineR)
pca.res <- PCA(df.data[,-1], graph=FALSE)

2. Créez un vecteur vcol.set qui contiendra les couleurs associés à chaque indidivu suivant s’il appartient au jeu d’apprentissage (en magenta) ou au jeu test (en bleu). Pour cela, :

• Créez le vecteur vcol.set qui contient 712 fois (nrow(df.data)) la couleur bleu.
  
• Dans ce vecteur, remplacez la valeur “bleu” des individus appartenant à l’échantillon d’apprentissage (ind.app) par la valeur “magenta”.

vcol.set <- rep("blue", length = nrow(df.data))
vcol.set[ind.app] <- "magenta"

3. Représentez la projection des individus sur les 2 premières composantes principales en colorant les individus suivant l’échantillon auquel ils appartiennent.

plot(pca.res, col.ind = vcol.set, label="none")
legend("topleft", legend=c("jeu d'apprentissage", "jeu test"), col=c("blue","magenta"), pch=19)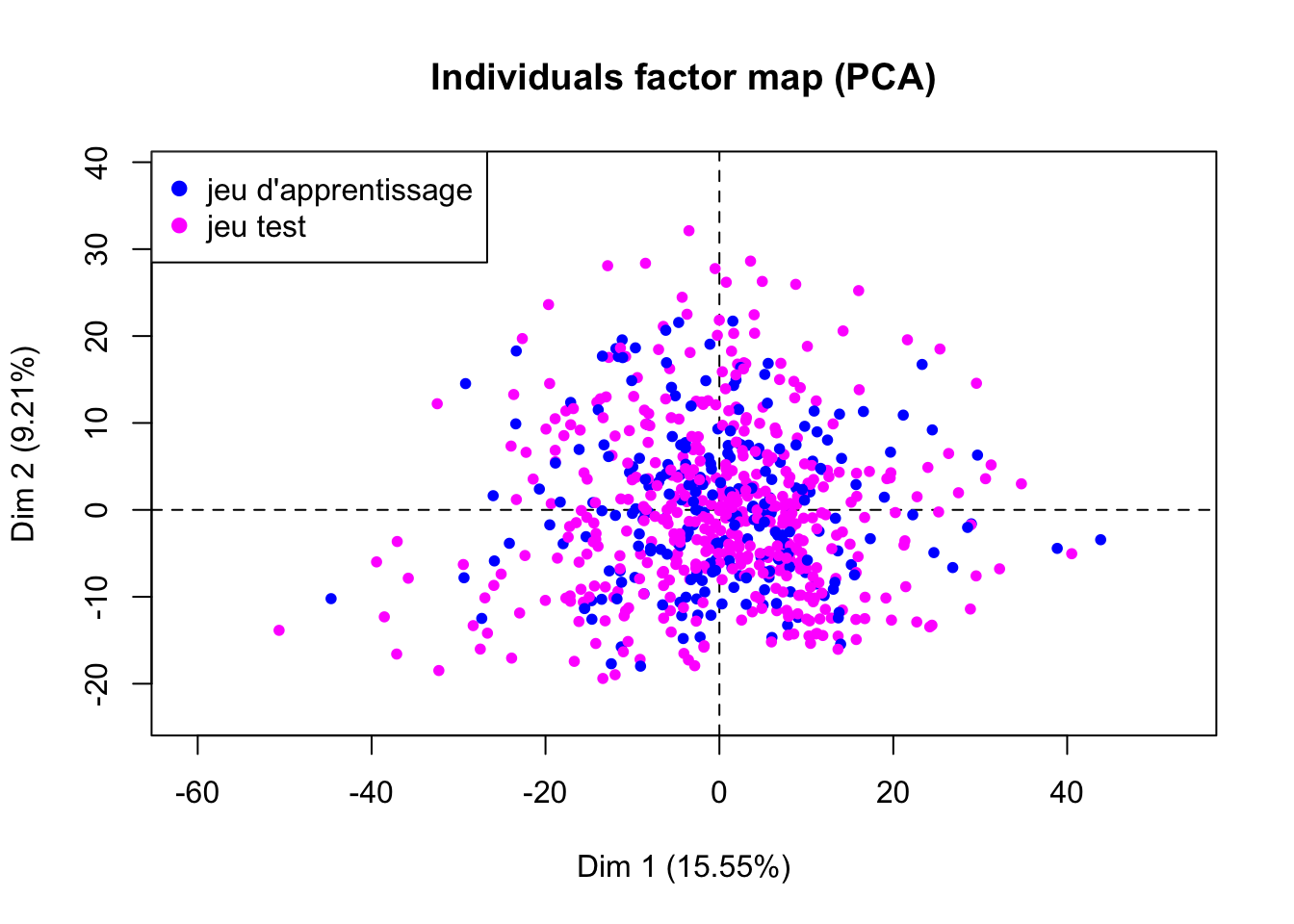

4. Déterminez la répartition des deux types de cancer dans les échantillons d’apprentissage et test.

par(mfrow=c(2,1))
barplot(table(mat.app[,"cancer.type"]), main="jeu d'apprentissage")
barplot(table(mat.test[,"cancer.type"]), main="jeu de test")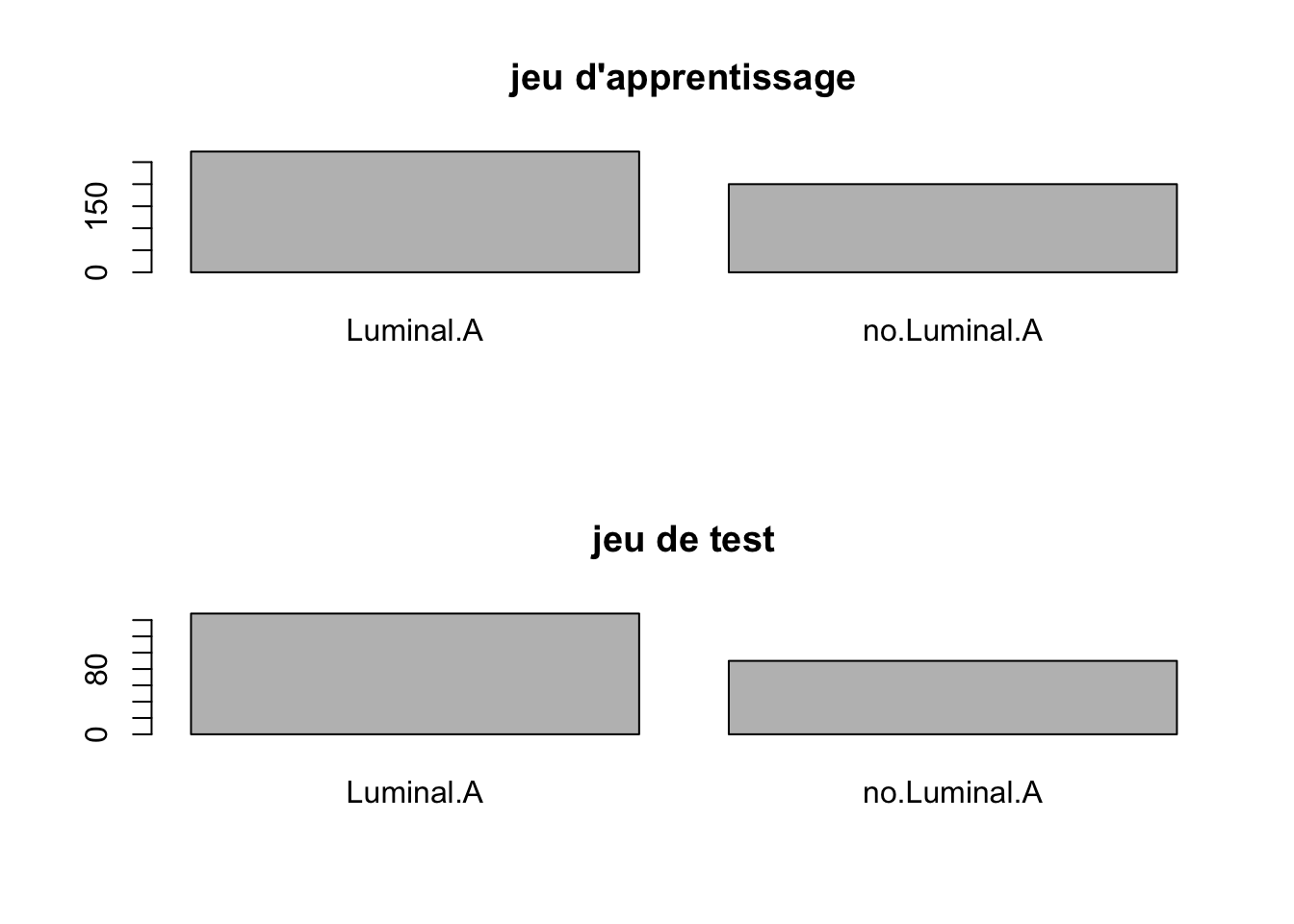

D’après les résultats obtenus, concluez sur la validité les échantillons d’apprentissage et test. Si vous concluez au fait que les deux échantillons ne sont pas valides, alors reprenez la procédure pour générer à nouveau des échantillons d’apprentissage et de test.

4 Prédiction du type de cancer en utilisant une approche de CART

1. A partir des données de l’échantillon d’apprentissage (mat.app), construisez un modèle de CART permettant de prédire le type de cancer (2 classes) en fonction de l’expression des gènes. Pour cela, utilisez la fonction rpart() de la librairie rpart.

library(rpart)
library(rpart.plot)

rpart.fit <-rpart(cancer.type~., data = mat.app)
rpart.fit

n= 474 

node), split, n, loss, yval, (yprob)
      * denotes terminal node

 1) root 474 200 Luminal.A (0.57805907 0.42194093)  
   2) ENSG00000029725.16>=19.01545 368 105 Luminal.A (0.71467391 0.28532609)  
     4) ENSG00000008838.18< 20.6166 351  88 Luminal.A (0.74928775 0.25071225)  
       8) ENSG00000043143.20>=16.82009 336  73 Luminal.A (0.78273810 0.21726190)  
        16) ENSG00000054598.6< 17.72386 318  59 Luminal.A (0.81446541 0.18553459)  
          32) ENSG00000025796.13< 19.96534 280  41 Luminal.A (0.85357143 0.14642857)  
            64) ENSG00000026103.20< 17.55003 273  36 Luminal.A (0.86813187 0.13186813) *
            65) ENSG00000026103.20>=17.55003 7   2 no.Luminal.A (0.28571429 0.71428571) *
          33) ENSG00000025796.13>=19.96534 38  18 Luminal.A (0.52631579 0.47368421)  
            66) ENSG00000033867.16>=18.38166 19   3 Luminal.A (0.84210526 0.15789474) *
            67) ENSG00000033867.16< 18.38166 19   4 no.Luminal.A (0.21052632 0.78947368) *
        17) ENSG00000054598.6>=17.72386 18   4 no.Luminal.A (0.22222222 0.77777778) *
       9) ENSG00000043143.20< 16.82009 15   0 no.Luminal.A (0.00000000 1.00000000) *
     5) ENSG00000008838.18>=20.6166 17   0 no.Luminal.A (0.00000000 1.00000000) *
   3) ENSG00000029725.16< 19.01545 106  11 no.Luminal.A (0.10377358 0.89622642)  
     6) ENSG00000004864.13< 16.80038 16   6 Luminal.A (0.62500000 0.37500000) *
     7) ENSG00000004864.13>=16.80038 90   1 no.Luminal.A (0.01111111 0.98888889) *

2. En utilisant la fonction prp() de la librairie rpart.plot(), représentez le modèle obtenu.

prp(rpart.fit, extra=2)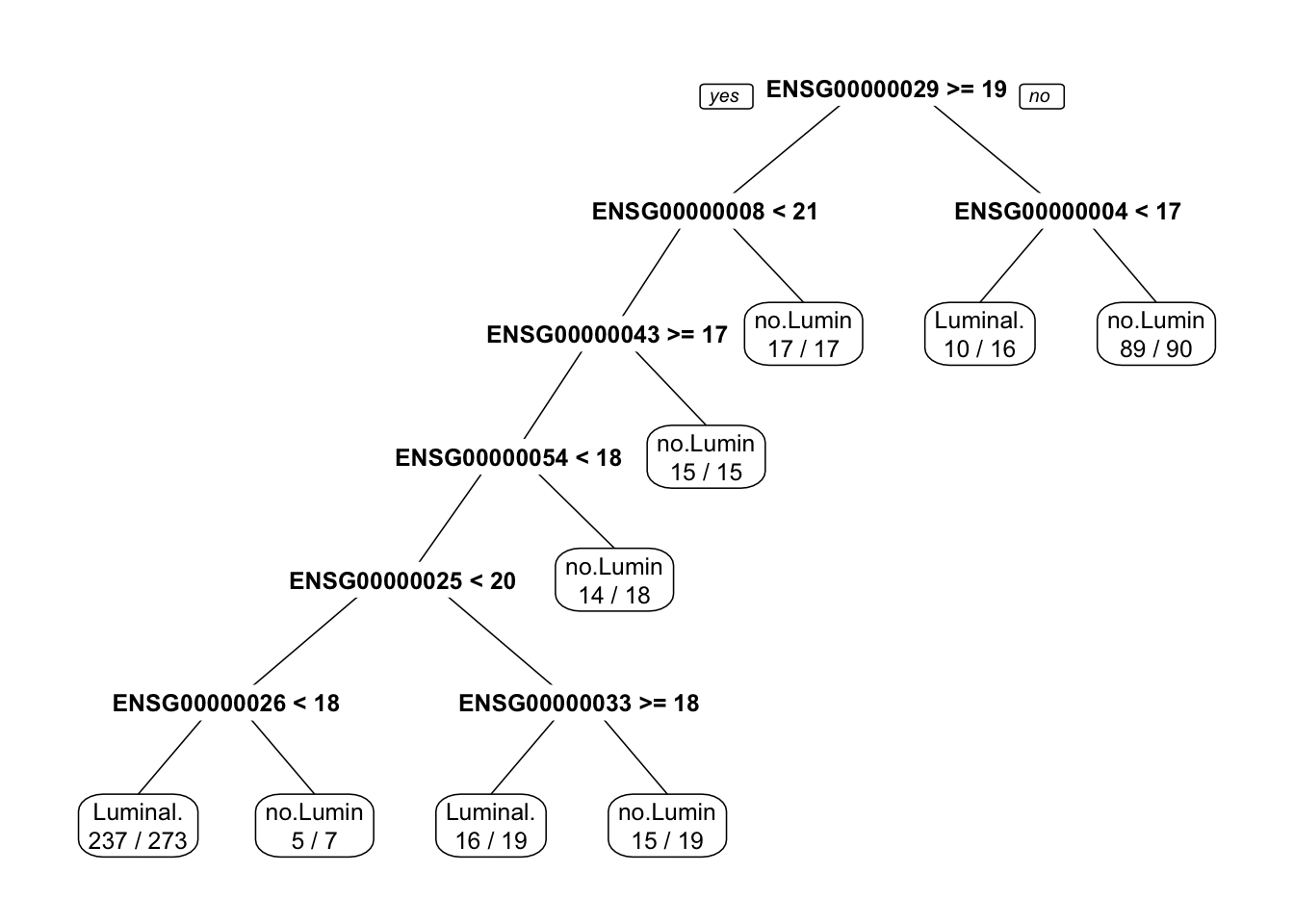

3. Sur les données de l’échantillon d’apprentissage calculez l’accuracy du modèle (=le taux de bien prédit) (\(Acc = \frac{VP+VN}{VP+VN+FP+FN}\)) .

• En utilisant la fonction predict(), prédisez le type de cancer pour chaque individu de l’échantillon d’apprentissage. N’oubliez pas de préciser l’argument type="class" pour préciser que vous faites de la classification. Stockez ces valeurs prédites dans le vecteur pred.app.
  Attention, la fonction predict()est une fonction générique. Dans ce cas, vous utilisez la fonction predict() appliquée à un objet rpart. Pour avoir plus d’informations sur les arguments de la fonction, vous devez utiliser l’aide de la fonction predict.rpart().

pred.app <- predict(rpart.fit, newdata = mat.app, type="class")

• A l’aide de la fonction table(), calculez la matrice de confusion entre les données prédites sur l’échantillon d’apprentissage (contenues dans le vecteur pred.app) et les vraies valeurs (contenues dans la colonne cancer.type du data.frame mat.app).

tc.rpart.app <- table(pred.app, mat.app[,"cancer.type"])
tc.rpart.app

              
pred.app       Luminal.A no.Luminal.A
  Luminal.A          263           45
  no.Luminal.A        11          155

• Calculez l’accuracy du modèle sur les données de l’apprentissage

acc.rpart.app <- sum(diag(tc.rpart.app))/sum(tc.rpart.app)
acc.rpart.app

[1] 0.8818565

4. En utilisant la même procédure que celle utilisée pour calculer l’accuracy sur le jeu d’apprentissage, calculez l’accuracy du modèle sur l’échantillon test

pred.test <- predict(rpart.fit, newdata = mat.test, type="class")

tc.rpart.test <- table(pred.test, mat.test[,"cancer.type"])
tc.rpart.test

              
pred.test      Luminal.A no.Luminal.A
  Luminal.A          127           33
  no.Luminal.A        21           57

acc.rpart.test <- sum(diag(tc.rpart.test))/sum(tc.rpart.test)
acc.rpart.test

[1] 0.7731092

En comparant les performances obtenues sur l’échantillon d’apprentissage et de test, vous constatez que les performances obtenues sur l’échantillon d’apprentissage (Acc=0.88) sont plus grandes que celles obtenues sur l’échantillon test (Acc=0.77). Ainsi, vous observez un phénomène de sur-apprentissage. Le modèle apprend très bien les données de l’échantillon d’apprentissage, mais prédit moins bien les données du jeu test.
Pour diminuer ce sur-apprentissage, une des solutions serait d’élaguer l’arbre, c’est-à-dire d’enlever certaines branches. Ainsi, le nouveau modèle obtenu serait moins performant sur les données d’apprentissage, mais plus performant sur les données du jeu test.

5 Prédiction du type de cancer en utilisant une approche de random forest

1. A partir des données de l’échantillon d’apprentissage, construisez une forêt aléatoire permettant de prédire le type de cancer (2 types) en fonction de l’expression des gènes.

• Pour cela, utilisez la fonction randomForest() de la librairie randomForest avec les paramètres mtry et mtree par défaut. Stockez le modèle dans l’objet rf.fit.

library(randomForest)
rf.fit <- randomForest(cancer.type~., data = mat.app)

• Affichez à l’écran le modèle créé.

rf.fit

Call:
 randomForest(formula = cancer.type ~ ., data = mat.app) 
               Type of random forest: classification
                     Number of trees: 500
No. of variables tried at each split: 31

        OOB estimate of  error rate: 20.25%
Confusion matrix:
             Luminal.A no.Luminal.A class.error
Luminal.A          248           26  0.09489051
no.Luminal.A        70          130  0.35000000

2. Choix de la valeur du paramètre ntree.

• L’objet rf.fit créé est une liste qui contient plusieurs éléments. L’élement err.rate contient les erreurs commises par le modèle contenant \(m\) arbres Représentez le taux d’erreur (Misclassification Rate) en fonction du nombre d’arbres présentant dans la forêt.

plot(rf.fit$err.rate[,1], type="l", xlab="nombre d'arbre dans la foret", ylab="taux d'erreur")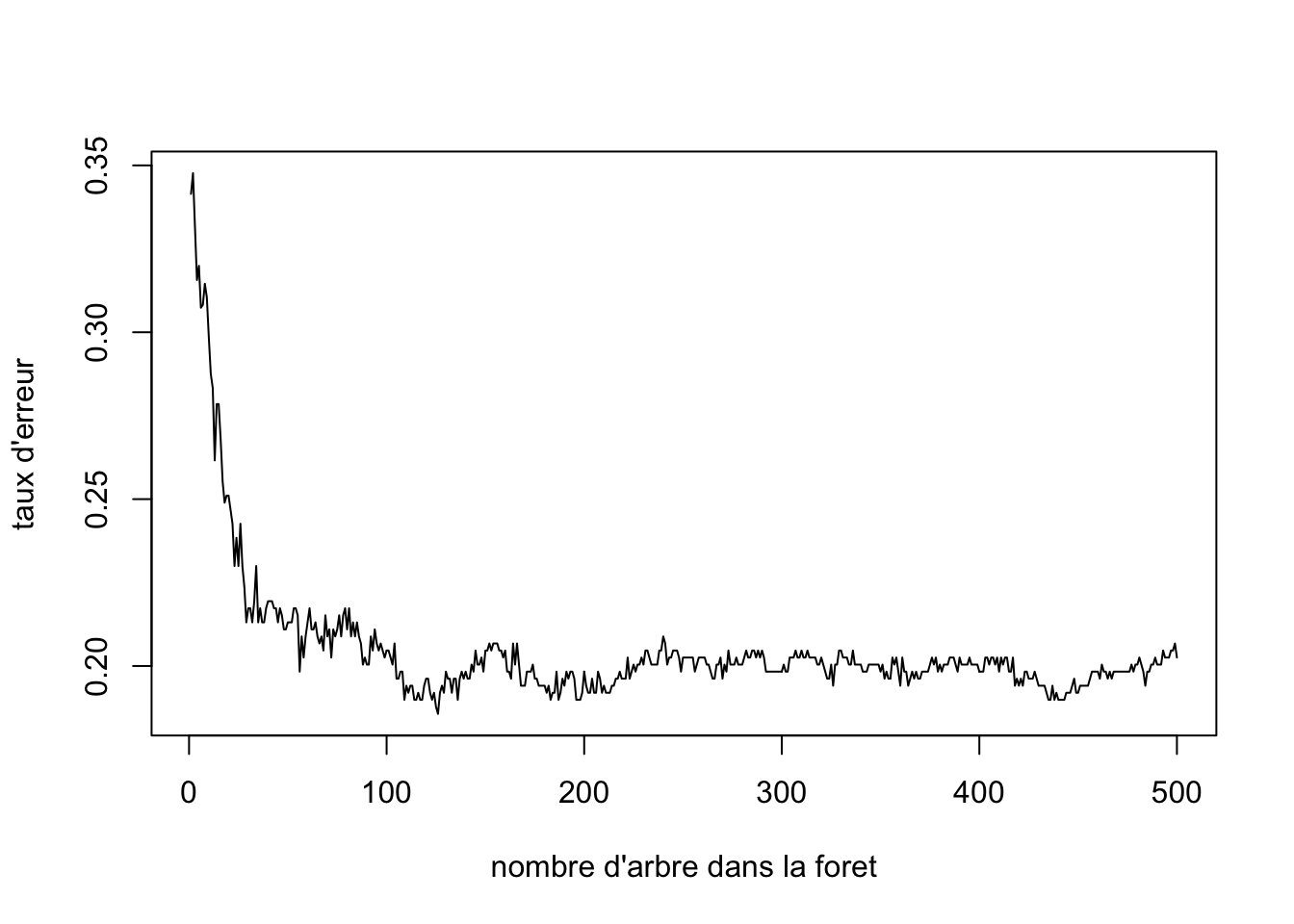

• A partir de ce graphique, choisissez le nombre d’arbres optimal, noté \(ntree_{opt}\).

ntree.opt <- 200

3. Choix de la valeur optimale pour le paramètre mtry.
   Remarque : cette étape est coûteuse en temps de calculs.

Pour trouver la valeur optimale de mtry, vous allez calculer plusieurs modèles en variant la valeur du paramètre mtry. Pour chaque modèle l’erreur commise par le modèle sera stockée dans un vecteur. La valeur optimale de mtry correspondra à la valeur du mtry du modèle donnant le plus faible taux d’erreur.

• Calculez les modèles pour des valeurs de mtry de 15, 30, 62, 124, 248, 350, 500, et la valeur de ntree optimale. Le taux d’erreur de chaque modèle sera stockée dans le vecteur v.err.

v.err <-  NULL
v.mtry <- c(15, 31, 62, 124, 248, 350, 500)
for(i in v.mtry){
    set.seed(123)
    rf.fit <- randomForest(cancer.type~., data = mat.app, ntree=ntree.opt, mtry=i)
    v.err <- c(v.err, rf.fit$err.rate[ntree.opt,1])
}

• Représentez graphiquement les erreurs commises par les modèles en fonction de la valeur de mtry.

plot(v.mtry, v.err, type ="b", xlab="mtry values", ylab="taux d'erreur", xaxt="n")
axis(1, at=v.mtry, labels=v.mtry, las=2)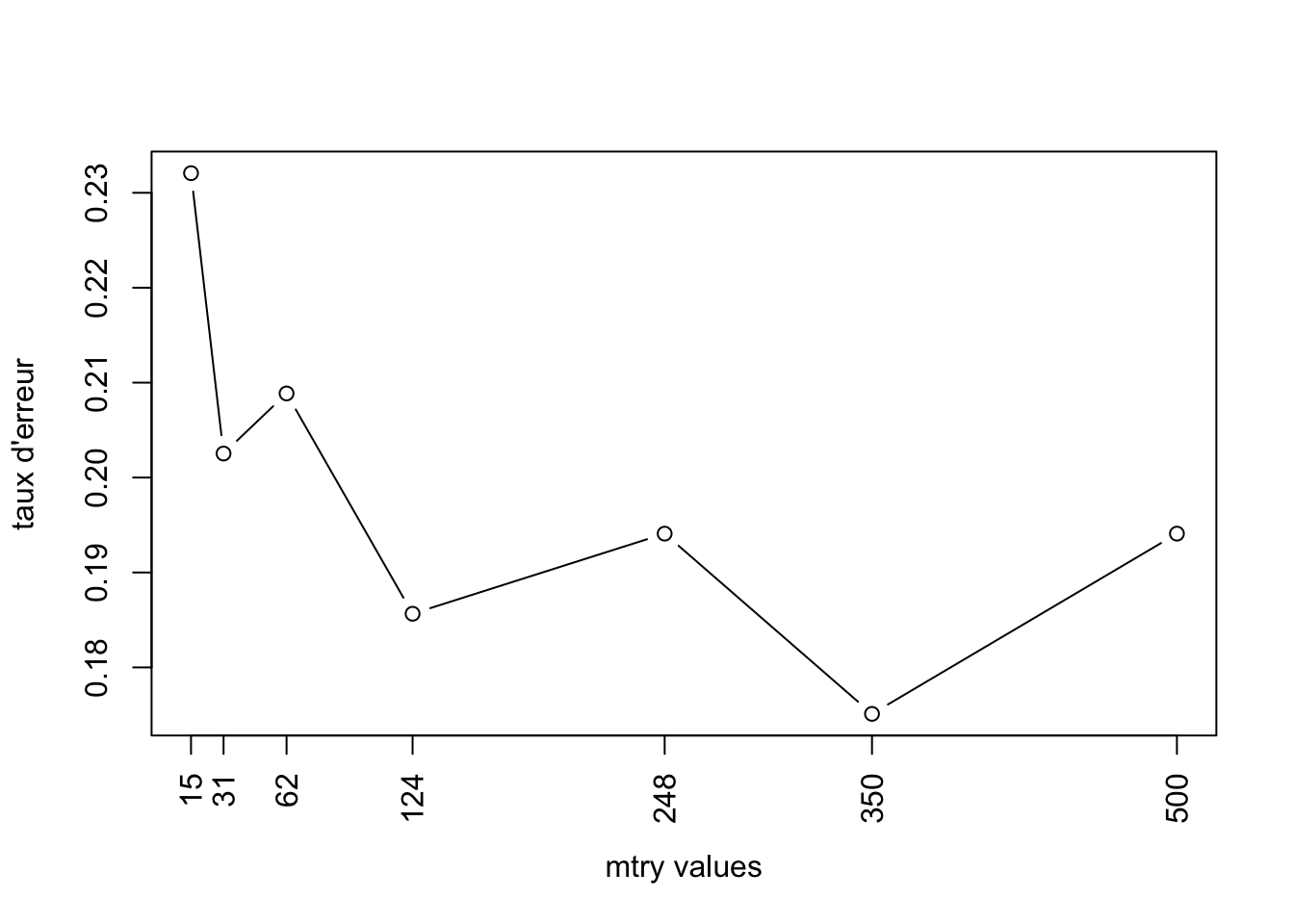

• A partir de ce graphique, déterminez la valeur optimale de mtry.

4. Calcul du modèle avec les paramètres optimaux.

• Calculez le modèle random forest sur l’échantillon d’apprentissage en utilisant les valeurs optimales des paramètres mtry et ntree. Dans la fonction randomForest(), ajouter l’argument importance=TRUE. Cet argument vous permettra de stocker l’importance des variables.

rf.fit <- randomForest(cancer.type~., data = mat.app, ntree=ntree.opt, mtry=248, importance=TRUE)

• Visualisez le modèle et la table de confusion obtenue sur les échantillons OOB.

rf.fit

Call:
 randomForest(formula = cancer.type ~ ., data = mat.app, ntree = ntree.opt,      mtry = 248, importance = TRUE) 
               Type of random forest: classification
                     Number of trees: 200
No. of variables tried at each split: 248

        OOB estimate of  error rate: 18.14%
Confusion matrix:
             Luminal.A no.Luminal.A class.error
Luminal.A          247           27  0.09854015
no.Luminal.A        59          141  0.29500000

3. Calcul des performances du modèle random forest

Pour comparer les performances de ce modèle, avec le modèle CART calculé précédemment, il faut calculer l’accuracy du modèle rf.fit sur les données des échantillons d’apprentissage et de test.

• Calculez l’accuracy du modèle sur les données de l’apprentissage

# Prédiction du type de cancer des individus du jeu d'apprentissage
pred.app <- predict(rf.fit, newdata = mat.app, type="class")

# matrice de confusion entre les données prédites sur l'échantillon d'apprentissage et les vraies valeurs.

tc.rf.app <- table(pred.app, mat.app[,"cancer.type"])
tc.rf.app

              
pred.app       Luminal.A no.Luminal.A
  Luminal.A          274            0
  no.Luminal.A         0          200

#  accuracy* du modèle sur les données de l'apprentissage
acc.rf.app <- sum(diag(tc.rf.app))/sum(tc.rf.app)
acc.rf.app

[1] 1

• Calcul de l’accuracy sur l’échantillon test

# prediction
pred.test <- predict(rf.fit, newdata = mat.test, type="class")

# table de confusion
tc.rf.test <- table(pred.test, mat.test[,"cancer.type"])
tc.rf.test

              
pred.test      Luminal.A no.Luminal.A
  Luminal.A          136           28
  no.Luminal.A        12           62

#accuracy
acc.rf.test <- sum(diag(tc.rf.test))/sum(tc.rf.test)
acc.rf.test

[1] 0.8319328

4. Comparez les performances des modèles de CART et de Random forest.

5. Etude de l’importance des variables (ici les gènes) dans le modèle.

• Représentez graphiquement l’importance de chaque gène en utilisant la fonction varImpPlot()

varImpPlot(rf.fit, n.var=50, cex = 0.7, type=1)

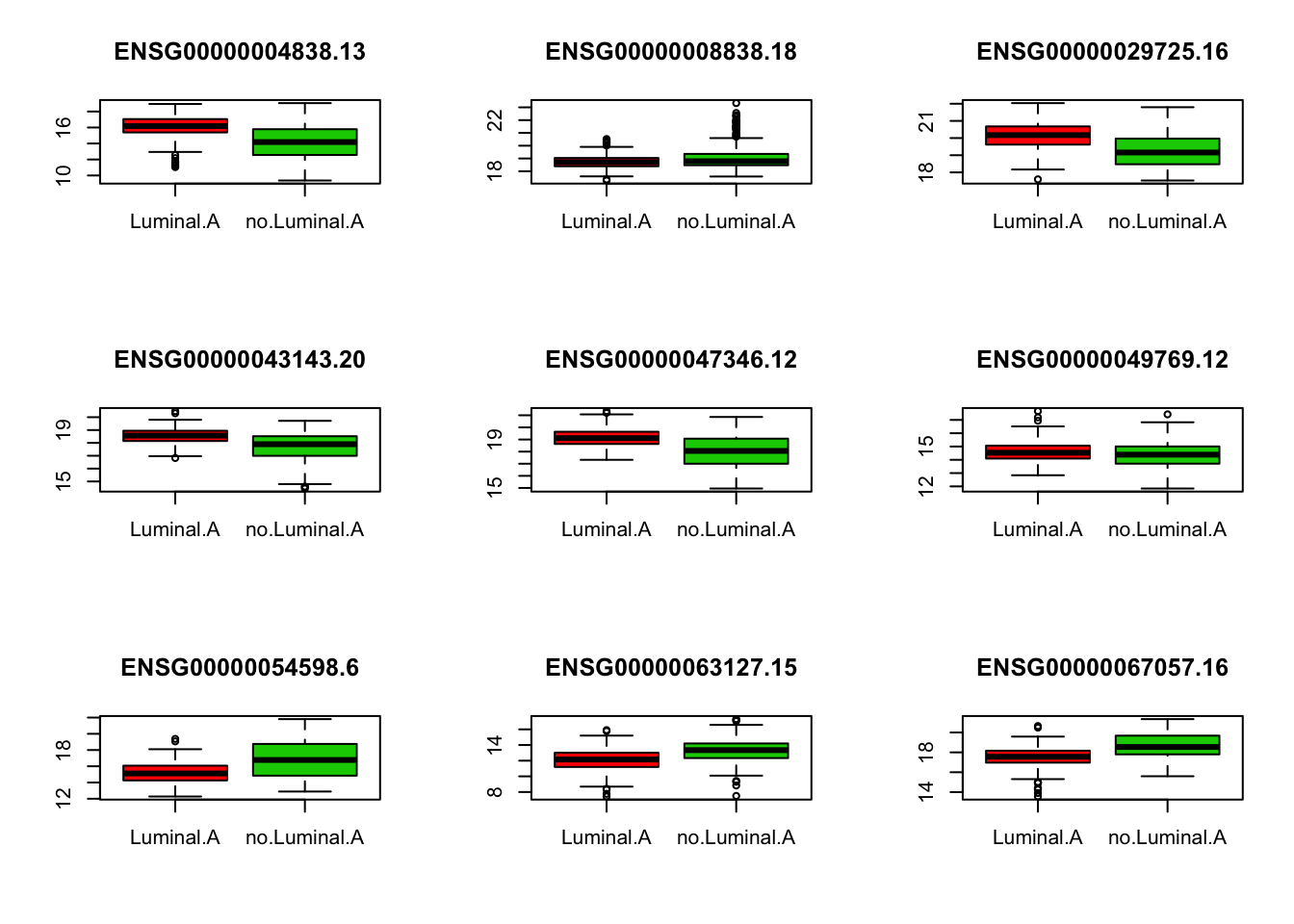
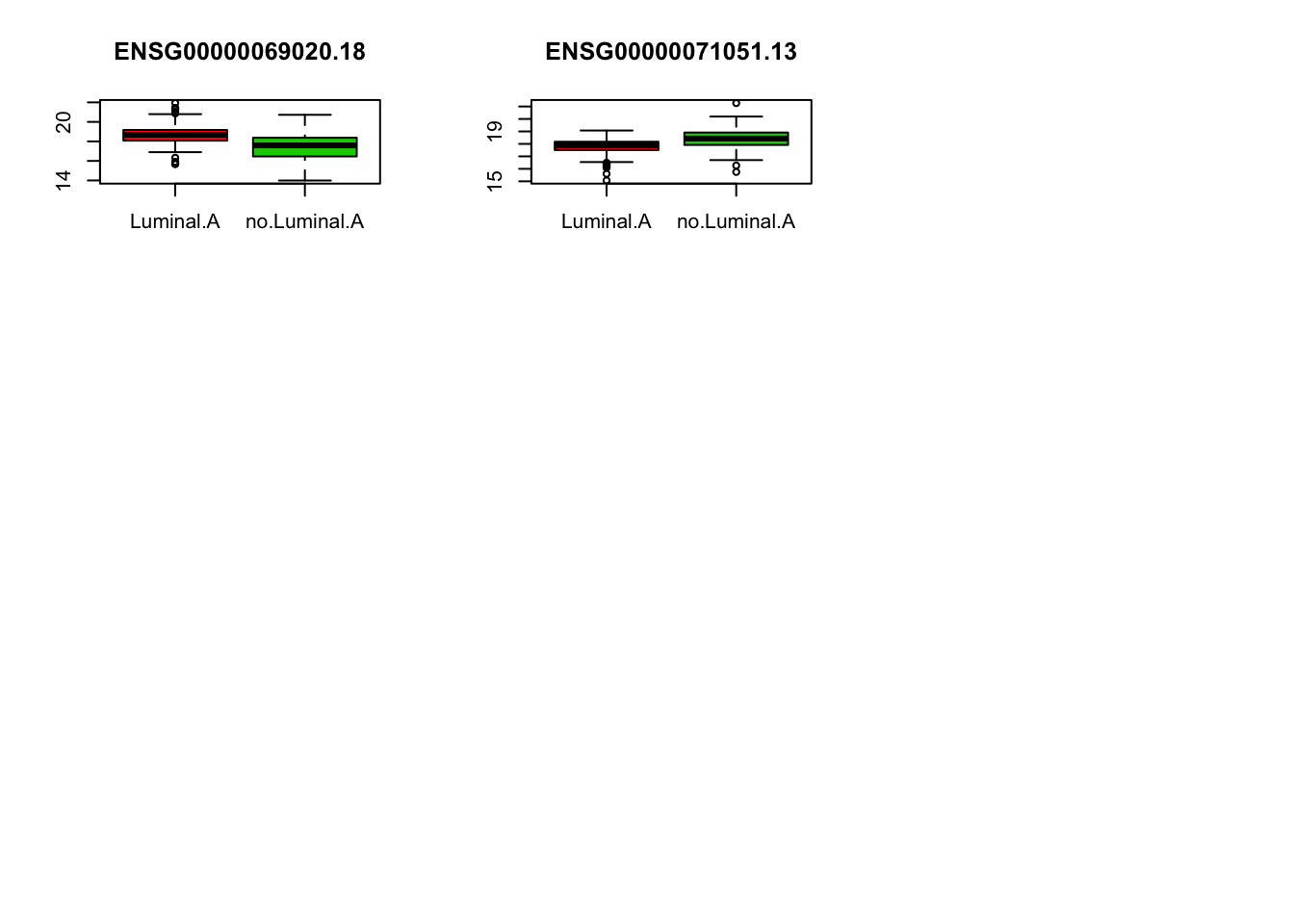
• Identifiez les gènes qui permettent de différentier le cancer Luminal.A des autres cancers.

• Pour chaque gene sélectionné, tracez la distribution de l’expression du gène chez les patients atteints d’un cancer de type Luminal.A et chez les autres patients d’après les données d’apprentissage.

v.imp <- importance(rf.fit)[,"MeanDecreaseAccuracy"]
gene.sel <- names(which(v.imp>4))

par(mfrow=c(3,3))
for(gene in gene.sel){
  boxplot(mat.app[,gene]~mat.app[,1],col=c(2,3), main=gene)
}

• Représentez la matrice des données en focalisant sur les gènes sélectionnées et en utilisant une heatmap.

#Trier les individus par type de cancer
ind.app.lA <- which(mat.app[,"cancer.type"]=="Luminal.A")
ind.tri <- c(ind.app.lA, setdiff(1:nrow(mat.app), ind.app.lA))
mat.app.tri <- t(mat.app[ind.tri, gene.sel])

# Compute mean value per gene
gene.means <- apply(mat.app.tri, 1, mean)
gene.sd <-  apply(mat.app.tri, 1, sd)

# Compute gene-wise centered expression values
BIC.expr.genes.centered <- mat.app.tri - gene.means

# Compute gene-wise centred + scaled expression values
BIC.expr.genes.standardized <- BIC.expr.genes.centered / gene.sd

## define a Blue - White - Red palette
frenchflag.palette <- colorRampPalette(c('dark blue','white','dark red'))

## Define a green - black - red palette
GBR.palette <- colorRampPalette(c('green','black','red'))

heatmap(as.matrix(BIC.expr.genes.standardized),
        zlim = c(-4,4), Colv=NA,
        distfun = function(x) as.dist(1 - cor(t(x), method = "spearman")), 
        hclustfun = function(x) hclust(x, method = "ward.D2"),
        labRow = NA, labCol = NA,  # DO not print the labels (unreadable anyway)
        col = GBR.palette(100),
        scale = "none")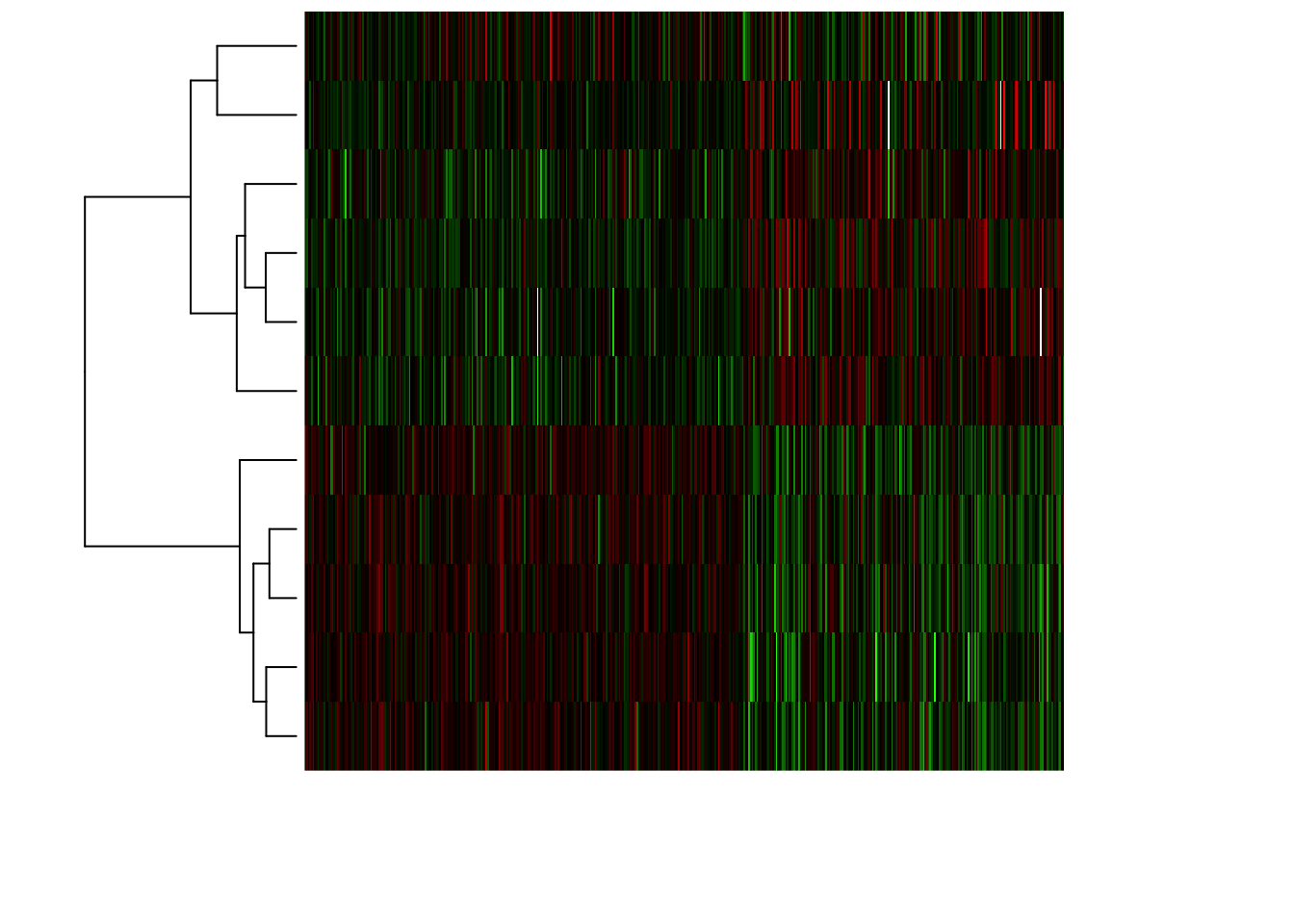

6 Prédiction du type de cancer en utilisant les Support Vecteur Machines

• utilisation avec formule R

library(e1071)
model=svm(cancer.type~., data=mat.app)

• utilisation classique

X=subset(mat.app, select = -cancer.type)
y=mat.app$cancer.type
model=svm(X,y)

• erreur d’apprentissage avec les paramètres par défaut

pred=predict(model, X)
table(pred, mat.app$cancer.type)

• surapprentissage avec gaussiennes très resserrées

model=svm(X,y,gamma=0.1)
pred=predict(model, X)
table(pred, mat.app$cancer.type)

• surapprentissage avec cost élevé

model=svm(X,y,cost=100)
pred=predict(model, X)
table(pred, mat.app$cancer.type)

• évaluation d’erreur de test (en surapprentissage)

Xtest=subset(mat.test, select = -cancer.type)
pred=predict(model, Xtest)
table(pred, mat.test$cancer.type)

• évaluation d’erreur de test (avec paramètres par défaut)

model=svm(X,y)
pred=predict(model, Xtest)
table(pred, mat.test$cancer.type)

7 Prédiction des échantillons classés comme “Unclassified”

Lors de l’étude du jeu de données initial, vous avez déterminé que 107 échantillons avaient été classés comme “Unclassified”. En utilisant les modèles de random forest et de SVM, prédisez le type de cancer pour ces individus. Comparez les résultats obtenus avec les deux modèles.

• Prédiction du type de cancer en utilisant le modèle random forest

mat.pred <- t(BIC.expr)
pred.uncl.rf <- predict(rf.fit, newdata = mat.pred[ind.uncl,])
table(pred.uncl.rf)

pred.uncl.rf
   Luminal.A no.Luminal.A 
          57           50 

• Prédiction du type de cancer en utilisant le modèle SVM

pred.uncl.svm <- predict(model, newdata = mat.pred[ind.uncl,])
table(pred.uncl.svm)

pred.uncl.svm
   Luminal.A no.Luminal.A 
          66           41 

• Calcul de la table de confusion entre les deux vecteurs de prédiction.

tc <- table(pred.uncl.rf, pred.uncl.svm)
tc

              pred.uncl.svm
pred.uncl.rf   Luminal.A no.Luminal.A
  Luminal.A           55            2
  no.Luminal.A        11           39

8 Prédiction des 4 types de cancer

1. Préparation du jeu de données

Créez un nouveau data.frame (df.data.4) qui contient les données d’expression de gènes contenu dans le data.frame BIC.expr.4 et le type de cancer pour chaque échantillon (définit en 4 types).

df.data.4 <- data.frame(as.character(BIC.sample.classes.4[,1]), t(BIC.expr.4))
df.data.4[,1] <- as.factor(df.data.4[,1])
colnames(df.data.4)[1] <- "cancer.type"

2. Préparation des échantillons d’apprentissage et de test

• En reprenant les individus sélectionnés pour la création de l’échantillon d’apprentissage ind.app, créez les data.frames mat.app.4 et mat.test.4 qui contiennent les données de l’échantillon d’apprentissage et celui de test.

mat.app.4 <- df.data.4[ind.app,]
dim(mat.app.4)

[1] 474 965

• Préparez l’échantillon test

mat.test.4 <- df.data.4[-ind.app,]
dim(mat.test.4)

[1] 238 965

3. Déterminez les paramètres mtry et ntree optimaux pour le random forest permettant de prédire les 4 types de cancer.

• Déterminez la valeur optimale du paramètre ntree.

rf.fit.4 <- randomForest(cancer.type~., data=mat.app.4)
plot(rf.fit.4$err.rate[,1], type="l", ylab = "taux d'erreur", xlab="nombre d'arbres")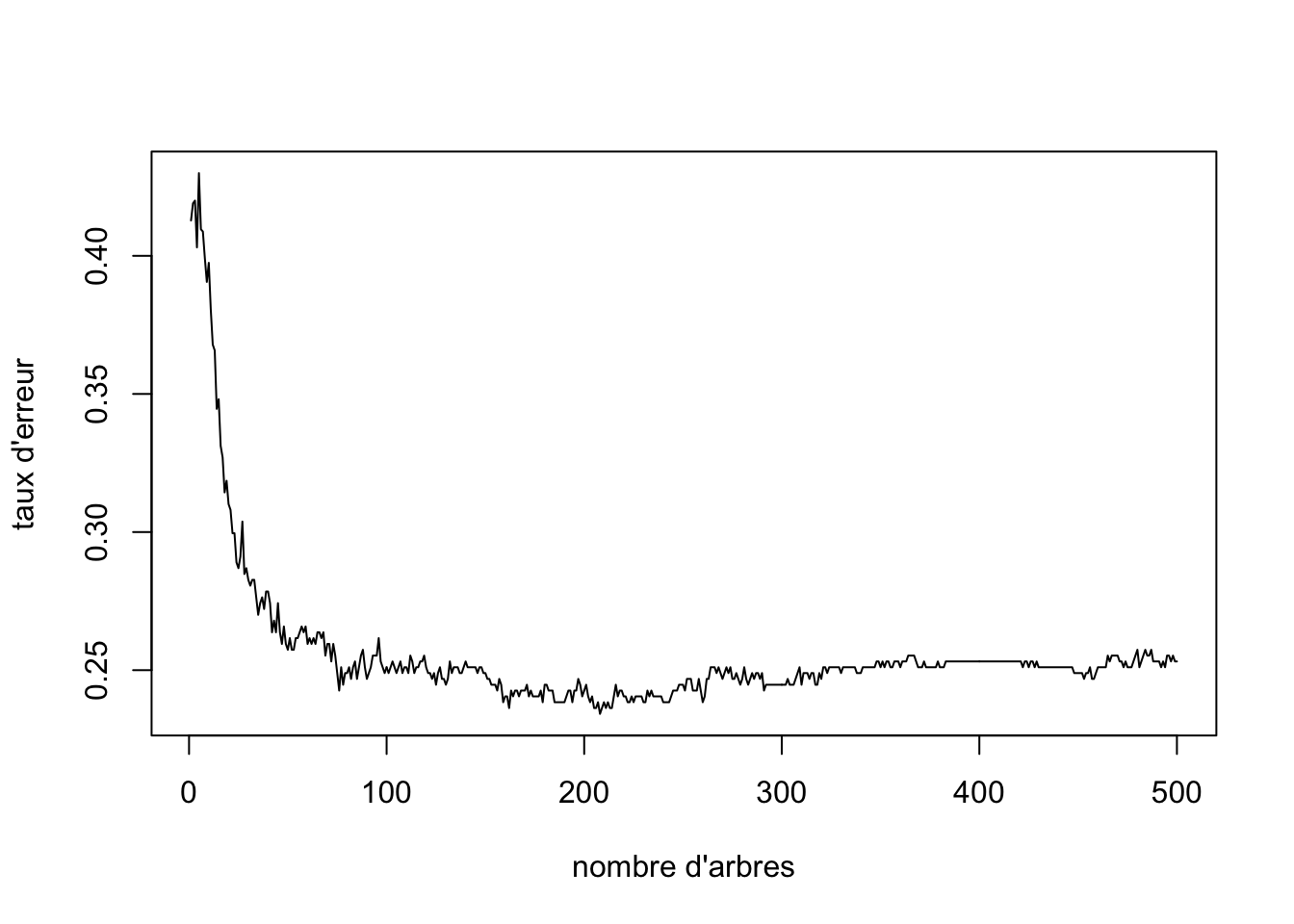

• Déterminez la valeur optimale du paramètre mtry.

v.err <-  NULL
v.mtry <- c(15, 31, 62, 124, 248, 350, 500)
for(i in v.mtry){
    set.seed(123)
    rf.fit <- randomForest(cancer.type~., data = mat.app.4, ntree=150, mtry=i)
    v.err <- c(v.err, rf.fit$err.rate[150,1])
}

plot(v.mtry, v.err, type ="b", xlab="mtry values", ylab="taux d'erreur", xaxt="n")
axis(1, at=v.mtry, labels=v.mtry, las=2)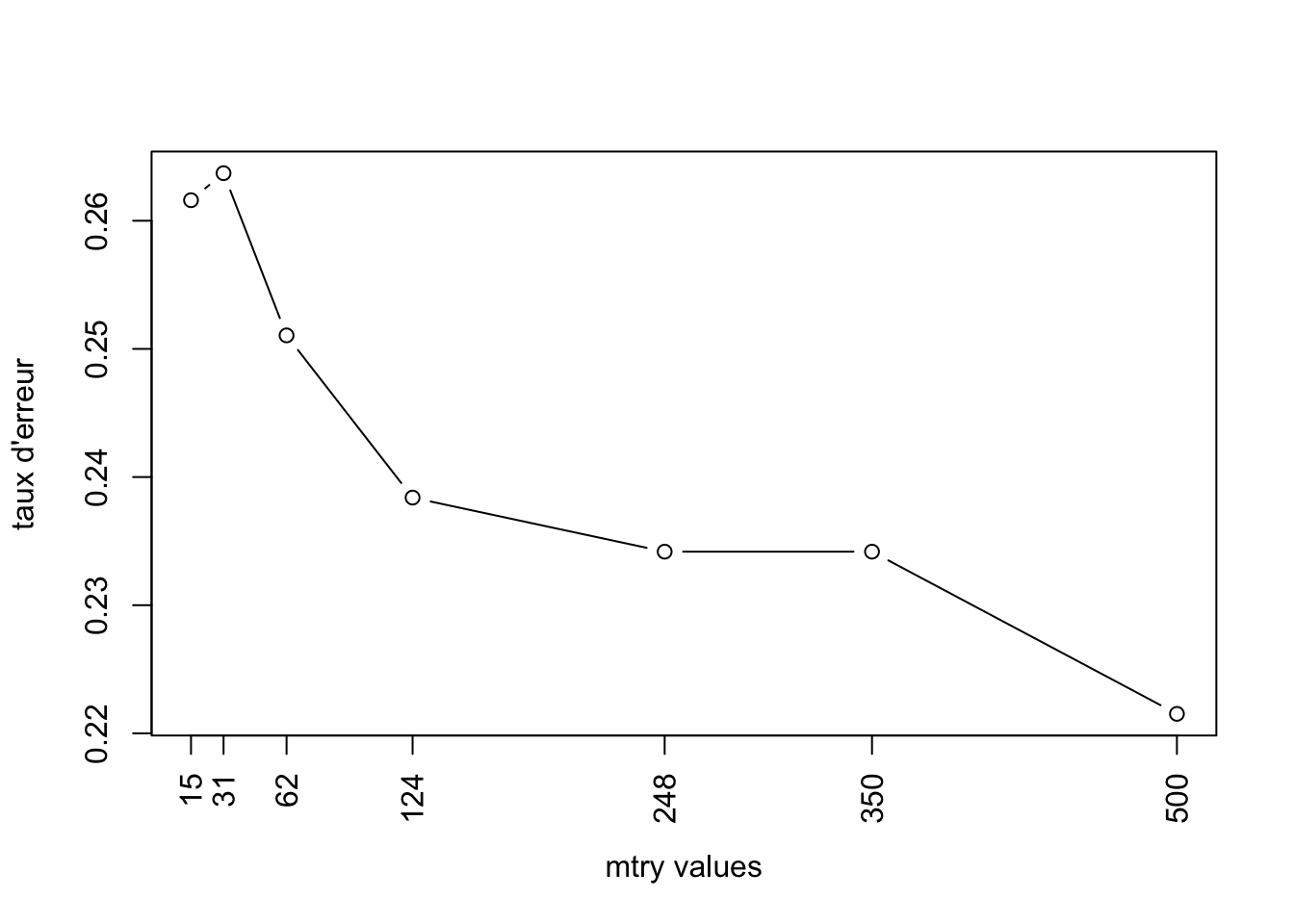

4. Calculez le modèle avec les paramètres optimaux.
   Calculez à nouveau le modèle sur l’échantillon d’apprentissage en utilisant les valeurs optimales des paramètres mtry et ntree. Dans la fonction randomForest(), ajouter l’argument importance=TRUE.

rf.fit.4 <- randomForest(cancer.type~., data = mat.app.4, ntree=150, mtry=124, importance=TRUE)

• Visualisez le modèle et la table de confusion obtenue sur les échantillons OOB.

rf.fit.4

Call:
 randomForest(formula = cancer.type ~ ., data = mat.app.4, ntree = 150,      mtry = 124, importance = TRUE) 
               Type of random forest: classification
                     Number of trees: 150
No. of variables tried at each split: 124

        OOB estimate of  error rate: 23.63%
Confusion matrix:
           Basal.like HER2pos Luminal.A Luminal.B class.error
Basal.like         74       1        15         2  0.19565217
HER2pos             9       2         7         8  0.92307692
Luminal.A           5       0       264         5  0.03649635
Luminal.B           1       0        59        22  0.73170732

5. Calculez les performances du modèle random forest sur l’échantillon d’apprentissage et de test.

• Calcul de l’accuracy sur l’échantillon d’apprentissage.

pred.app.4 <- predict(rf.fit.4, newdata = mat.app.4, type="class")
tc.rf4.app <- table(pred.app.4, mat.app.4[,"cancer.type"])
tc.rf4.app

            
pred.app.4   Basal.like HER2pos Luminal.A Luminal.B
  Basal.like         92       0         0         0
  HER2pos             0      26         0         0
  Luminal.A           0       0       274         0
  Luminal.B           0       0         0        82

acc.rf4.app <- sum(diag(tc.rf4.app))/sum(tc.rf4.app)
acc.rf4.app

[1] 1

• Calcul de l’accuracy sur l’échantillon test

pred.test.4 <- predict(rf.fit.4, newdata = mat.test.4, type="class")

tc.rf4.test <- table(pred.test.4, mat.test.4[,"cancer.type"])
tc.rf4.test

            
pred.test.4  Basal.like HER2pos Luminal.A Luminal.B
  Basal.like         35       1         0         0
  HER2pos             0       2         0         0
  Luminal.A           4       8       147        28
  Luminal.B           0       4         1         8

acc.rf4.test <- sum(diag(tc.rf4.test))/sum(tc.rf4.test)
acc.rf4.test

[1] 0.8067227

6. Etude de l’importance des descripteurs dans le modèle.

• Représentez graphiquement la valeur d’importance des différents gènes en utilisant la fonction varImpPlot()

varImpPlot(rf.fit.4, n.var=50, cex = 0.6, type=1)