Le but de ce TP est de développer des modèles statistiques pour prédire le type de cancer en utilisant les données de l’étude TCGA (The Cancer Genome Atlas; https://cancergenome.nih.gov/) qui regroupent des données RNA-seq de patients atteints d’un cancer du sein (Breast Invasice Cancer or BIC). Cela regroupe deux types de cancers invasifs: les carcinomes ductal et lobulaire. Les articles originaux de ces études sont ici: https://www.nature.com/articles/nature11412 et https://www.cell.com/cell/fulltext/S0092-8674(15)01195-2

Pour ce TP, vous utiliserez les données suivantes :

fichier BIC_log2-norm-counts_edgeR_DEG_top_1000.tsv.gz qui correspond au fichier d’expression pour les 1000 gènes (lignes) les plus significatifs pour 819 échantillons (colonnes).
fichier BIC_sample-classes.tsv.gz qui contient les étiquettes des 819 échantillons.

Sur le serveur Rstudio de l’IFB-core-cluster, les données sont dans le répertoire : /shared/projects/du_bii_2019/data/module3/seance4/BIC/

si vous travaillez sur une installation locale, vous pouvez télécharger un clone de ce cours

mkdir -p ~/DUBii_clones
cd ~/DUBii_clones
git clone https://github.com/DU-Bii/module-3-Stat-R.git
cd module-3-Stat/

Au cours de ce TP, vous allez développer différents modèles statistiques :

Dans un premier temps, vous construirez des modèles pour prédire si le cancer est du type “lumina.A” ou pas en utilisant :
- un modèle CART,
- un modèle de random forest,
- un modèle de SVM,
Dans un second temps, vous construirez un modèle de random forest pour prédire un des 4 types de cancer : Basal.like, HER2pos, Luminal.A ou Luminal.B.

1 Préparation des données

Ouvrez le fichier d’expression des gènes en utilisant la commande read.table(). Stockez ce data.frame dans l’objet BIC.expr. Vérifiez la taille du data.frame généré en utilisant la commande dim().

data.folder <- "/shared/projects/dubii2020/data/module3/seance7/BIC"
# data.folder <- "data/BIC"

## THIS DATA SET WILL BE TESTED FOR A FUTURE PRACTICAL
# data.folder <- "/shared/projects/dubii2020/trainers/github_clones/study-cases/Homo_sapiens/TCGA_study-case/TCGA_AML_data"

BIC.expr.file <- file.path(data.folder, "BIC_log2-norm-counts_edgeR_DEG_top_1000.tsv.gz")
#BIC.expr.file <- file.path(data.folder, "AML_counts_filtered-genes.tsv.gz")
BIC.expr <- read.table(file = BIC.expr.file, header = TRUE)
dim(BIC.expr)

[1] 1000  819

Ouvrez le fichier qui contient les étiquettes des échantillons en utilisant la commande read.table(). Stockez ce data.frame dans l’objet BIC.sample.classes.

BIC.sample.classes <- read.table(file.path(data.folder, "BIC_sample-classes.tsv.gz"),header = TRUE)
#BIC.sample.classes <- read.table(file.path(data.folder, "BIC_sample-classes_simple.csv"),header = TRUE)
#BIC.sample.classes <- read.table(file.path(data.folder, "AML_sample-classes.tsv.gz"),header = TRUE)

Vérifiez le nombre d’échantillons disponibles dans ce jeu de données.

dim(BIC.sample.classes)

[1] 819   4

Le fichier contient 819 lignes et 4 colonnes. Chaque ligne correspond à un échantillon.

Le tableau contient non seulement les classes (colonne cancer.type) mais également les valeurs positive/negative pour trois gènes utilisés comme marqueurs pour diagnostiquer le type de cancer, indiqués dans les en-têtes de colonnes: ER1, PR1 et Her2.

head(BIC.sample.classes)

                                      cancer.type      ER1      PR1     Her2
1AB92ADA-637E-4A42-A39A-70CEEEA41AE3    Luminal.A Positive Positive Negative
DA98A67C-F11F-41D3-8223-1161EBFF8B58 Unclassified Positive Negative Negative
06CCFD0F-7FB8-471E-B823-C7876582D6FC      HER2pos Negative Negative Positive
A33B2F42-6EC6-4FB2-8BE5-542407A0382E Unclassified Positive Negative Negative
D021A258-8713-4383-9DCA-45E2F54A0411    Luminal.A Positive Positive Negative
C705FA90-D9AA-4949-BACA-1C022A14CB03    Luminal.A Positive Positive Negative

Déterminez le type de variables disponibles dans ce jeu de données en utilisant la fonction summary().

summary(BIC.sample.classes)

       cancer.type        ER1            PR1            Her2    
 Basal.like  :131   Negative:184   Negative:267   Negative:631  
 HER2pos     : 41   Positive:635   Positive:552   Positive:188  
 Luminal.A   :422                                               
 Luminal.B   :118                                               
 Unclassified:107

La première colonne du data.frame BIC.sample.classes renseigne sur le type de cancer de chaque échantillon.

Comme vous pouvez le voir, il y a 5 types de cancer, dont un “Unclassified”. Lors de la prédiction du type de cancer, ce type risque de biaiser les résultats. Nous allons donc temporairement supprimer ces échantillons des jeux de données, mais nous reviendrons dessus à la fin du TP, car ils constituent une excellente application de l’apprentissage automatique. En effet, si un modèle (classifieur entraîné) s’avère donner de bons résultats lors de l’évaluation (training / testing), nous pourrons l’utiliser pour prédire le type de cancer de ces échantillons de type “Unclassified”.

Supprimez les échantillons correspondant au type Unclassified dans les deux data.frames.

En utilisant la fonction which(), identifiez les lignes du data.frame BIC.sample.classes qui correspondent au type Unclassified. Vérifiez que vous avez bien sélectionné 107 individus.

## Generate a Boolean vector indicating which samples are unclassfied
unclassified <- BIC.sample.classes$cancer.type == "Unclassified"

## Count the number of genes having or not the unclassified label
table(unclassified)

unclassified
FALSE  TRUE 
  712   107

## Get the indices of the corresponding rowss
ind.uncl <- which(unclassified)

## Count
length(ind.uncl)

[1] 107

Supprimez ces individus dans le data.frame BIC.sample.classes en utilisant l’indexation négative. Vérifiez la taille du nouveau data.frame. Le nouveau data.frame se nommera BIC.sample.classes.4.

## Create a separate data frame 
BIC.sample.classes.4 <- BIC.sample.classes[-ind.uncl,]
dim(BIC.sample.classes.4)

[1] 712   4

Supprimez les échantillons correspondant au type Unclassified du data.frame BIC.expr. Attention, dans le data.frame BIC.expr les échantillons sont présentés en colonnes.

BIC.expr.4 <- BIC.expr[, -ind.uncl] 
dim(BIC.expr.4)

[1] 1000  712

Pour construire les premiers modèles, vous n’allez pas utiliser les quatre types de cancers, mais seulement deux :
- Luminal.A,
- non Luminal.A : qui correspondent aux autres types. Vous allez donc transformer la colonne cancer.type du data.frame BIC.sample.classes.2 en une variable qualitative à deux classes : “Luminal.A” ou “no.Luminal.A”.

Créez le vecteur new.type qui contient 712 fois (nrow(BIC.sample.classes.2)) la valeur “Luminal.A”.

new.type <- rep("Luminal.A", length = nrow(BIC.sample.classes.4))

Identifiez les individus qui ne contiennent pas “Luminal.A” dans la première colonne (colonne cancer.type) du data.frame BIC.sample.classes.4.

ind.noLA <- which(BIC.sample.classes.4[,"cancer.type"]!="Luminal.A")

Pour ces individus, assignez la valeur “no.Luminal.A” au vecteur new.type.

new.type[ind.noLA] = "no.Luminal.A"

Remplacez la colonne cancer.type du data.frame BIC.sample.classes.2 par le vecteur new.type que vous aurez transformé en facteur (fonction as.factor())

BIC.sample.classes.2 <- BIC.sample.classes.4
BIC.sample.classes.2[,"cancer.type"] = as.factor(new.type)

Suppression des variables corrélées

Une des étapes du nettoyage du jeu de données correspond à supprimer les variables (ici les gènes) corrélées. Pour cela, vous allez utiliser la fonction findCorrelation() de la librairie caret. Cette fonction prend en entrée la matrice de corrélation entre les variables et le seuil de corrélation à partir duquel on considère que deux variables sont corrélées.

Calculez la matrice de corrélation entre les gènes différentiellement exprimés. Comme dans le data.frame BIC.expr.4 les gènes sont en lignes, pensez à transposer votre data.frame.

mat.cor <- cor(t(BIC.expr.4))
dim(mat.cor)

[1] 1000 1000

# corrplot::corrplot(mat.cor)

Identifiez les gènes à supprimer en utilisant un seuil de corrléation de 0.8 et la fonction findCorrelation(). Combien de gènes allez vous supprimer.

dim(mat.cor)

[1] 1000 1000

var.supp <- findCorrelation(mat.cor, cutoff = 0.8)
length(var.supp)

[1] 36

print(var.supp)

 [1] 136 150 250 301 365 391 501 513 585 697 790 821 829 830 832 846 902 929 994  37 217 139 255  45 287 157 247 554 288 437 307 164 729 755 145 151

Supprimez ces gènes du data.frame BIC.expr.4.

BIC.expr.4 <- BIC.expr.4[-var.supp,]
dim(BIC.expr.4)

[1] 964 712

Pour créer les modèles de prédiction, il est nécessaire d’avoir un data.frame qui regroupe pour chaque échantillon les gènes et son type de cancer.

Créez le data.frame df.data qui contient :
- en lignes ; les échantillons
- en colonnes : les gènes et le type de cancer.

Pour cela, utilisez la commande data.frame().
+ La première colonne de votre data.frame df.data doit correspondre aux types de cancer.
+ les colonnes 2 à 965 doivent correspondre aux gènes.

df.data <- data.frame(BIC.sample.classes.2[,1], t(BIC.expr.4))
dim(df.data)

[1] 712 965

Assignez “cancer.type” comme nom de colonne à la première colonne de df.data.

colnames(df.data)[1] <- "cancer.type"
# View(df.data)
kable(df.data[1:10, 1:5])

	cancer.type	ENSG00000000003.14	ENSG00000000419.12	ENSG00000000457.13	ENSG00000000460.16
X1AB92ADA.637E.4A42.A39A.70CEEEA41AE3	Luminal.A	16.52775	17.50349	17.96040	16.77151
X06CCFD0F.7FB8.471E.B823.C7876582D6FC	no.Luminal.A	18.67677	18.15315	17.51914	16.85386
D021A258.8713.4383.9DCA.45E2F54A0411	Luminal.A	17.75758	16.58779	19.09800	18.15086
C705FA90.D9AA.4949.BACA.1C022A14CB03	Luminal.A	18.83214	17.81858	19.01201	17.85704
X85380A2D.9951.4D4B.A2A4.6F5F2AFC54E3	Luminal.A	18.52097	17.30436	18.63385	17.61519
F53A9C63.1AF7.4CBC.B8B7.4AA7AAED3364	Luminal.A	16.26266	18.52012	17.55598	17.35059
X13EF5323.EAD9.4BC7.8AC4.33875BF12E17	no.Luminal.A	17.38771	17.97410	18.22298	17.05569
X079EACA1.0319.4B54.B20B.673F4576C69D	no.Luminal.A	16.95062	17.75839	18.04384	17.74923
X2E63B18E.FDC1.414C.9291.492D3D380232	no.Luminal.A	18.66658	17.17837	17.21481	16.00784
F5303C4B.7008.44AF.8D22.0BA38750DEA2	no.Luminal.A	18.52184	17.05632	17.93438	17.02691

2 Préparation des échantillons d’apprentissage et de test

L’échantillon d’apprentissage est l’échantillon qui va permettre d’apprendre les modèles. Il sera constitué de 2/3 des échantillons sélectionnés de manière aléatoire.
L’échantillon de test est l’échantillon qui va permettre d’estimer les performances non biaisées des modèles. Il sera constitué du 1/3 des échantillons restant.

En utilisant la fonction sample() créez un vecteur qui contient le numéro d’indice de 2/3 des individus choisis aléatoirement. Ces individus vont constituter le jeu d’apprentissage.

ind.app <- sample(1:nrow(df.data), size = 2/3 * nrow(df.data))

Créez le data.frame mat.app qui contient les valeurs d’expression des gènes et le type de cancer pour les individus choisis aléatoirement. Cette matrice correspond au jeu d’apprentissage.

mat.app <- df.data[ind.app,]
dim(mat.app)

[1] 474 965

Créez le data.frame mat.test qui contient les valeurs d’expression de gènes et le type de cancer pour les individus restants (1/3). Cette matrice correspond au jeu test.

mat.test <- df.data[-ind.app,]
dim(mat.test)

[1] 238 965

3 Validation des deux échantillons.

Calculez une analyse en composantes principale en utilisant le data.frame df.data. Pour cela, utilisez la fonction PCA() de la librairie FactoMineR. Pensez à ne pas prendre en compte la colonne renseignant sur le type de cancer car ce n’est pas une variable quantitative.

library(FactoMineR)
pca.res <- PCA(df.data[, -1], graph = FALSE)

Créez un vecteur vcol.set qui contiendra les couleurs associés à chaque indidivu suivant s’il appartient au jeu d’apprentissage (en magenta) ou au jeu test (en bleu). Pour cela, :

Créez le vecteur vcol.set qui contient 712 fois (nrow(df.data)) la couleur bleu.
Dans ce vecteur, remplacez la valeur “bleu” des individus appartenant à l’échantillon d’apprentissage (ind.app) par la valeur “magenta”.

vcol.set <- rep("blue", length = nrow(df.data))
vcol.set[ind.app] <- "magenta"

Représentez la projection des individus sur les 2 premières composantes principales en colorant les individus suivant l’échantillon auquel ils appartiennent.

plot(pca.res, 
     habillage = "ind", 
     col.hab = vcol.set, graph.type = "classic",
     label = "none")
legend("topleft",
       legend = c("training set", 
                  "test set"),
       col = c("blue","magenta"), pch = 19)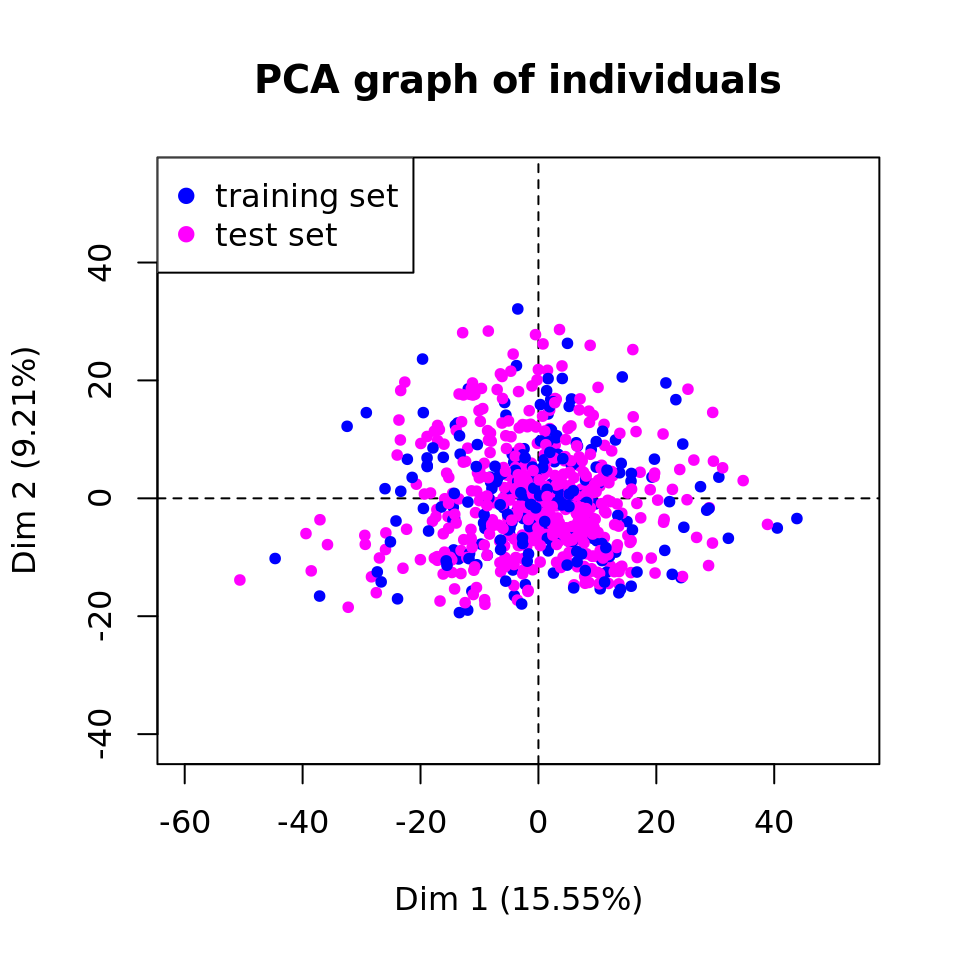

Projection of the samples on the two first principal components.

Déterminez la répartition des deux types de cancer dans les échantillons d’apprentissage et test.

par(mfrow=c(2,1))
barplot(table(mat.app[,"cancer.type"]), main="jeu d'apprentissage")
barplot(table(mat.test[,"cancer.type"]), main="jeu de test")

Répartition des deux types de cancers dans les échantillons d’apprentissage et de test

par(mfrow=c(1,1))

D’après les résultats obtenus, concluez sur la validité les échantillons d’apprentissage et test. Si vous concluez au fait que les deux échantillons ne sont pas valides, alors reprenez la procédure pour générer à nouveau des échantillons d’apprentissage et de test.

4 Prédiction du type de cancer en utilisant une approche de CART

A partir des données de l’échantillon d’apprentissage (mat.app), construisez un modèle de CART permettant de prédire le type de cancer (2 classes) en fonction de l’expression des gènes. Pour cela, utilisez la fonction rpart() de la librairie rpart.

library(rpart)
library(rpart.plot)
rpart.fit <- rpart(cancer.type ~ ., data = mat.app)
rpart.fit

n= 474 

node), split, n, loss, yval, (yprob)
      * denotes terminal node

 1) root 474 194 Luminal.A (0.59071730 0.40928270)  
   2) ENSG00000004838.13>=15.52558 263  47 Luminal.A (0.82129278 0.17870722)  
     4) ENSG00000008838.18< 20.69176 253  37 Luminal.A (0.85375494 0.14624506)  
       8) ENSG00000047346.12>=17.66518 237  27 Luminal.A (0.88607595 0.11392405)  
        16) ENSG00000005448.16>=15.18117 228  21 Luminal.A (0.90789474 0.09210526)  
          32) ENSG00000005238.19>=15.99697 220  16 Luminal.A (0.92727273 0.07272727)  
            64) ENSG00000037637.10>=16.91799 212  11 Luminal.A (0.94811321 0.05188679) *
            65) ENSG00000037637.10< 16.91799 8   3 no.Luminal.A (0.37500000 0.62500000) *
          33) ENSG00000005238.19< 15.99697 8   3 no.Luminal.A (0.37500000 0.62500000) *
        17) ENSG00000005448.16< 15.18117 9   3 no.Luminal.A (0.33333333 0.66666667) *
       9) ENSG00000047346.12< 17.66518 16   6 no.Luminal.A (0.37500000 0.62500000) *
     5) ENSG00000008838.18>=20.69176 10   0 no.Luminal.A (0.00000000 1.00000000) *
   3) ENSG00000004838.13< 15.52558 211  64 no.Luminal.A (0.30331754 0.69668246)  
     6) ENSG00000029725.16>=18.94642 132  64 no.Luminal.A (0.48484848 0.51515152)  
      12) ENSG00000010404.17>=19.6765 77  25 Luminal.A (0.67532468 0.32467532)  
        24) ENSG00000006652.13< 18.37902 67  16 Luminal.A (0.76119403 0.23880597)  
          48) ENSG00000062716.11>=19.24657 58   9 Luminal.A (0.84482759 0.15517241)  
            96) ENSG00000040531.14>=16.32803 47   2 Luminal.A (0.95744681 0.04255319) *
            97) ENSG00000040531.14< 16.32803 11   4 no.Luminal.A (0.36363636 0.63636364) *
          49) ENSG00000062716.11< 19.24657 9   2 no.Luminal.A (0.22222222 0.77777778) *
        25) ENSG00000006652.13>=18.37902 10   1 no.Luminal.A (0.10000000 0.90000000) *
      13) ENSG00000010404.17< 19.6765 55  12 no.Luminal.A (0.21818182 0.78181818)  
        26) ENSG00000030419.16>=17.28779 9   2 Luminal.A (0.77777778 0.22222222) *
        27) ENSG00000030419.16< 17.28779 46   5 no.Luminal.A (0.10869565 0.89130435) *
     7) ENSG00000029725.16< 18.94642 79   0 no.Luminal.A (0.00000000 1.00000000) *

En utilisant la fonction prp() de la librairie rpart.plot(), représentez le modèle obtenu.

prp(rpart.fit, extra = 2)

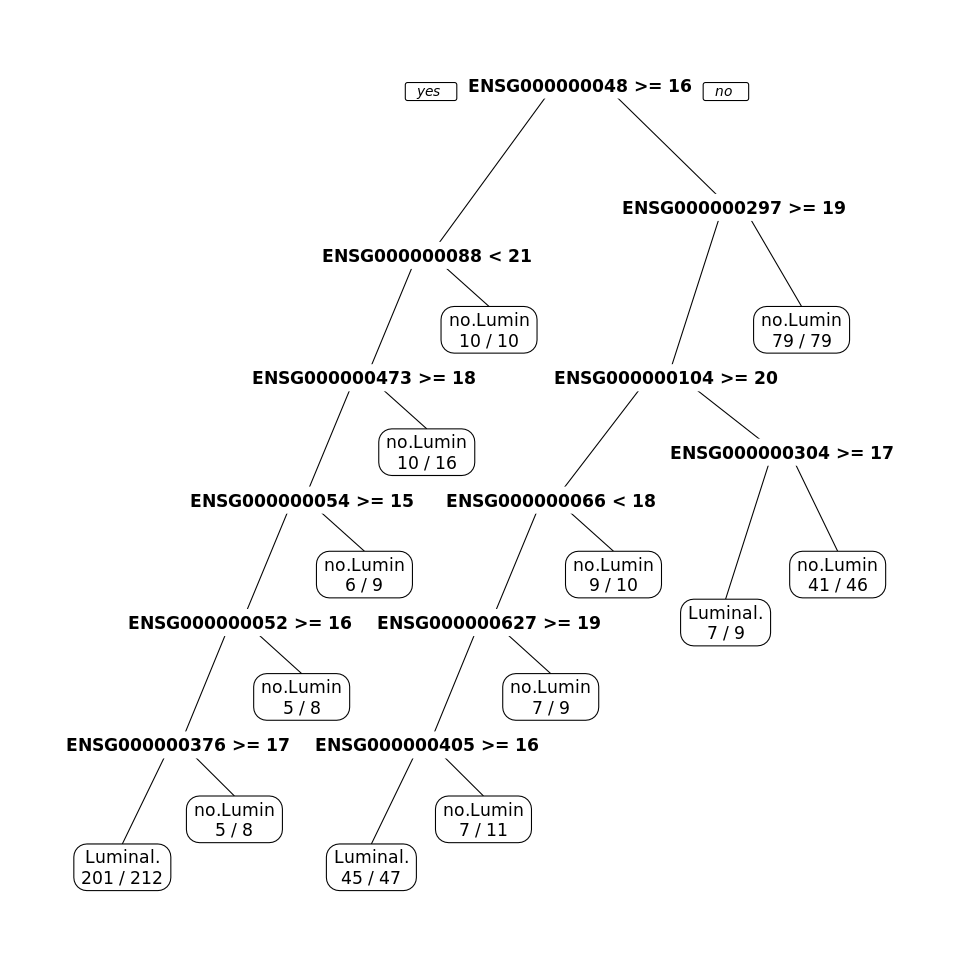
Model

Sur les données de l’échantillon d’apprentissage calculez l’accuracy du modèle (=le taux de bien prédit) (\(Acc = \frac{VP+VN}{VP+VN+FP+FN}\)) .

En utilisant la fonction predict(), prédisez le type de cancer pour chaque individu de l’échantillon d’apprentissage. N’oubliez pas de préciser l’argument type="class" pour préciser que vous faites de la classification. Stockez ces valeurs prédites dans le vecteur pred.app.
Attention, la fonction predict()est une fonction générique. Dans ce cas, vous utilisez la fonction predict() appliquée à un objet rpart. Pour avoir plus d’informations sur les arguments de la fonction, vous devez utiliser l’aide de la fonction predict.rpart().

pred.app <- predict(rpart.fit, newdata = mat.app, type = "class")

A l’aide de la fonction table(), calculez la matrice de confusion entre les données prédites sur l’échantillon d’apprentissage (contenues dans le vecteur pred.app) et les vraies valeurs (contenues dans la colonne cancer.type du data.frame mat.app).

tc.rpart.app <- table(pred.app, mat.app[,"cancer.type"])
kable(tc.rpart.app, caption = "Confusion table of the CART model for the predictions obtained with the training set (learning errors). ")

Confusion table of the CART model for the predictions obtained with the training set (learning errors).
	Luminal.A	no.Luminal.A
Luminal.A	253	15
no.Luminal.A	27	179

Calculez l’accuracy du modèle sur les données de l’apprentissage

acc.rpart.app <- sum(diag(tc.rpart.app))/sum(tc.rpart.app)
acc.rpart.app

[1] 0.9113924

En utilisant la même procédure que celle utilisée pour calculer l’accuracy sur le jeu d’apprentissage, calculez l’accuracy du modèle sur l’échantillon test

pred.test <- predict(rpart.fit, newdata = mat.test, type = "class")

tc.rpart.test <- table(pred.test, mat.test[,"cancer.type"])
kable(tc.rpart.test, caption = "Confusion table for the predictions obtained from the testing set. ")

Confusion table for the predictions obtained from the testing set.
	Luminal.A	no.Luminal.A
Luminal.A	104	24
no.Luminal.A	38	72

acc.rpart.test <- sum(diag(tc.rpart.test))/sum(tc.rpart.test)
acc.rpart.test

[1] 0.7394958

En comparant les performances obtenues sur l’échantillon d’apprentissage et de test, vous constatez que les performances obtenues sur l’échantillon d’apprentissage (Acc=0.91) sont plus grandes que celles obtenues sur l’échantillon test (Acc=0.74). Ainsi, vous observez un phénomène de sur-apprentissage. Le modèle apprend très bien les données de l’échantillon d’apprentissage, mais prédit moins bien les données du jeu test.
Pour diminuer ce sur-apprentissage, une des solutions serait d’élaguer l’arbre, c’est-à-dire d’enlever certaines branches. Ainsi, le nouveau modèle obtenu serait moins performant sur les données d’apprentissage, mais plus performant sur les données du jeu test.

5 Prédiction du type de cancer en utilisant une approche de random forest

A partir des données de l’échantillon d’apprentissage, construisez une forêt aléatoire permettant de prédire le type de cancer (2 types) en fonction de l’expression des gènes.

Pour cela, utilisez la fonction randomForest() de la librairie randomForest avec les paramètres mtry et mtree par défaut. Stockez le modèle dans l’objet rf.fit.

library(randomForest)
rf.fit <- randomForest(cancer.type ~ ., data = mat.app)

Affichez à l’écran le modèle créé.

print(rf.fit)


Call:
 randomForest(formula = cancer.type ~ ., data = mat.app) 
               Type of random forest: classification
                     Number of trees: 500
No. of variables tried at each split: 31

        OOB estimate of  error rate: 18.35%
Confusion matrix:
             Luminal.A no.Luminal.A class.error
Luminal.A          261           19  0.06785714
no.Luminal.A        68          126  0.35051546

kable(as.data.frame(rf.fit$confusion), 
      caption = "Confusion table obtained by Random Forest on the training set (learning errors).  ")

Confusion table obtained by Random Forest on the training set (learning errors).
	Luminal.A	no.Luminal.A	class.error
Luminal.A	261	19	0.0678571
no.Luminal.A	68	126	0.3505155

Choix de la valeur du paramètre ntree.

L’objet rf.fit créé est une liste qui contient plusieurs éléments. L’élement err.rate contient les erreurs commises par le modèle contenant \(m\) arbres Représentez le taux d’erreur (Misclassification Rate) en fonction du nombre d’arbres présentant dans la forêt.

plot(rf.fit$err.rate[,1], 
     type = "l", 
     main = "Random forest: impact of the number of trees",
     xlab = "Number of trees in the forest", 
     ylab = "Misclassification error rate")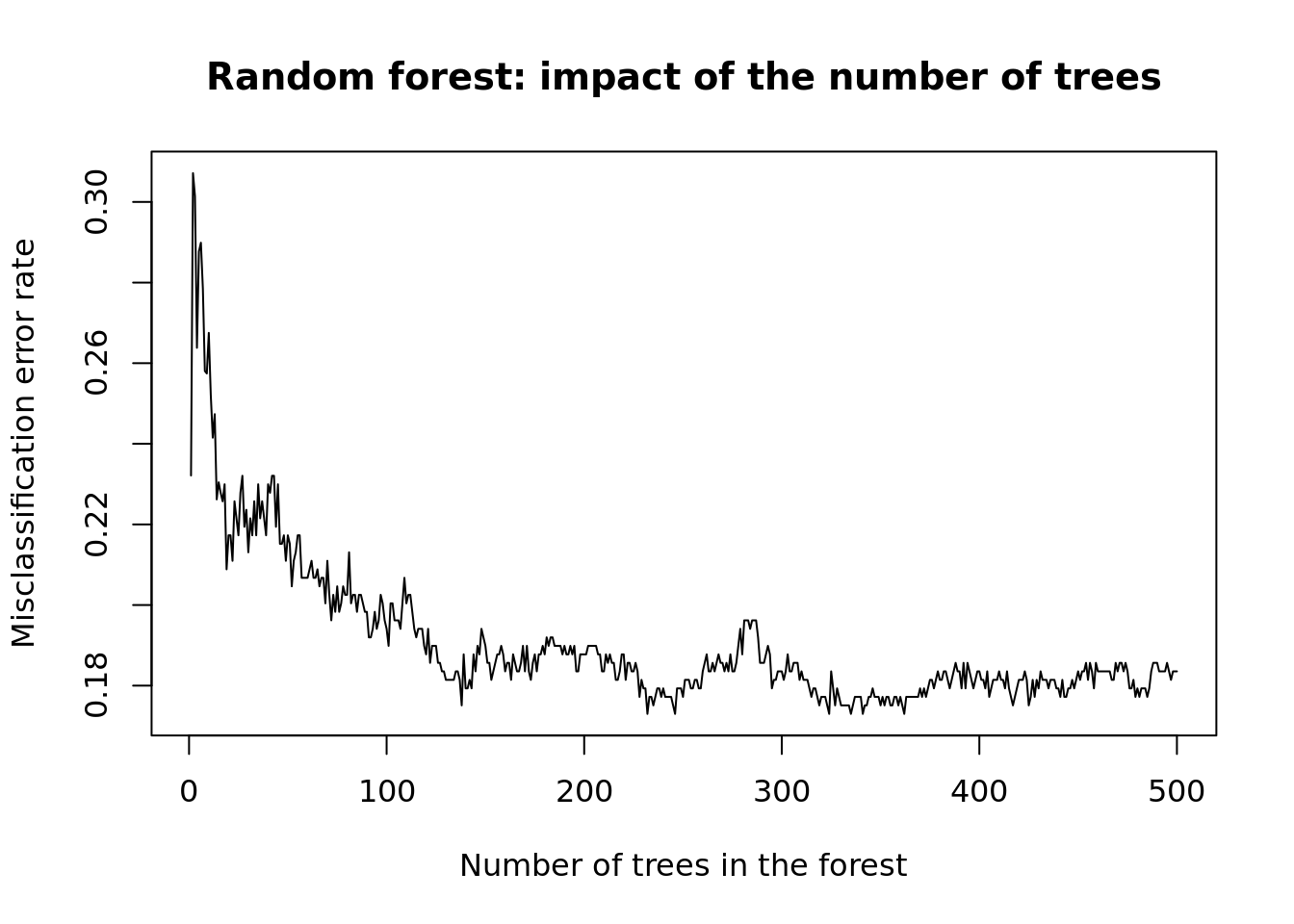

Random forest: impact of the number of tree on the misclassification error rate (MER)

A partir de ce graphique, choisissez le nombre d’arbres optimal, noté \(ntree_{opt}\).

ntree.opt <- 200

Choix de la valeur optimale pour le paramètre mtry.

Remarque : cette étape est coûteuse en temps de calculs.

Pour trouver la valeur optimale de mtry, vous allez calculer plusieurs modèles en variant la valeur du paramètre mtry. Pour chaque modèle l’erreur commise par le modèle sera stockée dans un vecteur. La valeur optimale de mtry correspondra à la valeur du mtry du modèle donnant le plus faible taux d’erreur.

Calculez les modèles pour des valeurs de mtry de 15, 30, 62, 124, 248, 350, 500, et la valeur de ntree optimale. Le taux d’erreur de chaque modèle sera stockée dans le vecteur v.err.

v.err <-  NULL
v.mtry <- c(15, 31, 62, 124, 248, 350, 500)
for(i in v.mtry){
    set.seed(123)
    rf.fit <- randomForest(cancer.type~., data = mat.app, ntree=ntree.opt, mtry=i)
    v.err <- c(v.err, rf.fit$err.rate[ntree.opt,1])
}

Représentez graphiquement les erreurs commises par les modèles en fonction de la valeur de mtry.

plot(v.mtry, v.err, type ="b", xlab="mtry values", ylab="taux d'erreur", xaxt="n")
axis(1, at=v.mtry, labels=v.mtry, las=2)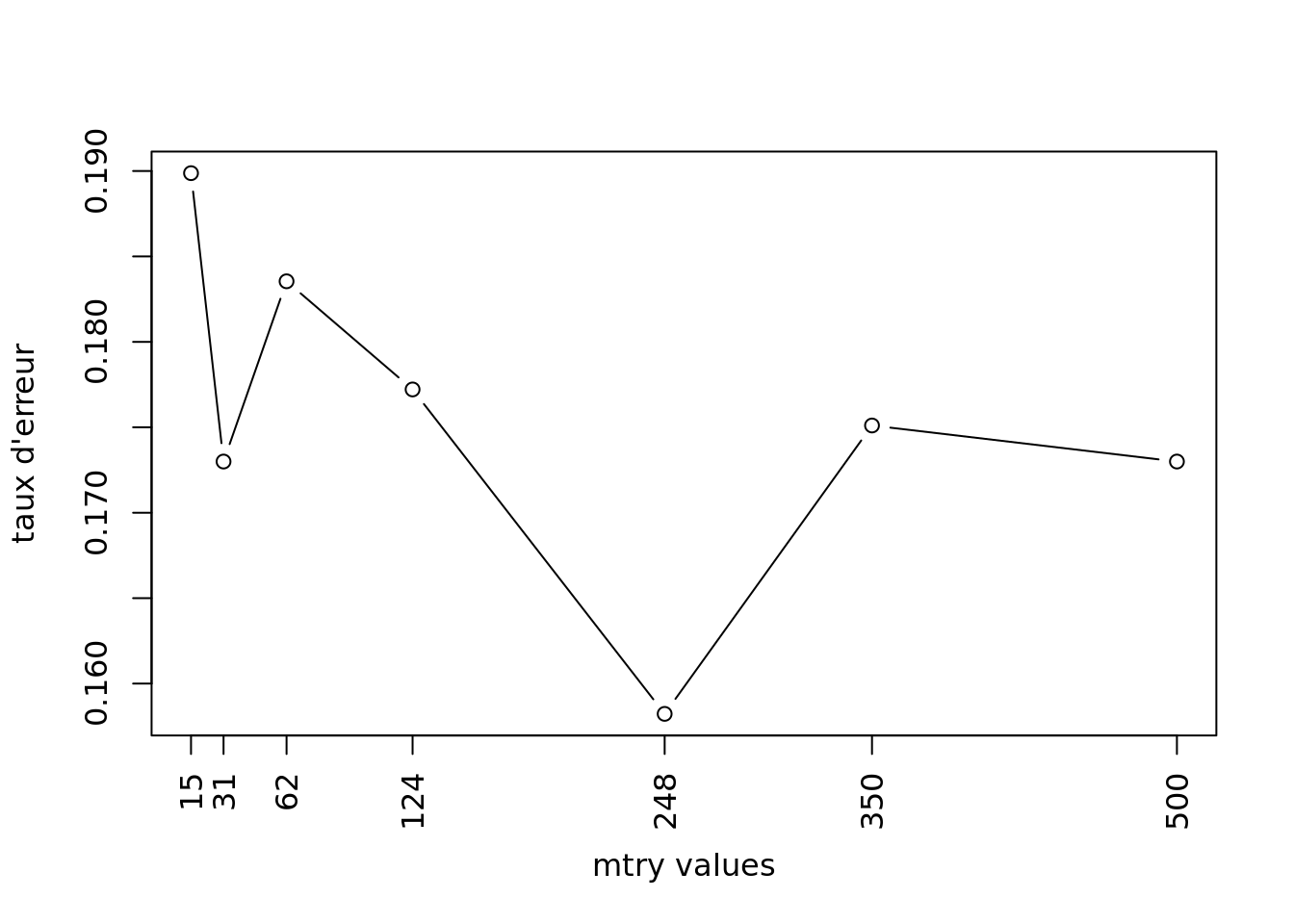

A partir de ce graphique, déterminez la valeur optimale de mtry.

Calcul du modèle avec les paramètres optimaux.

Calculez le modèle random forest sur l’échantillon d’apprentissage en utilisant les valeurs optimales des paramètres mtry et ntree. Dans la fonction randomForest(), ajouter l’argument importance=TRUE. Cet argument vous permettra de stocker l’importance des variables.

rf.fit <- randomForest(cancer.type~., data = mat.app, ntree=ntree.opt, mtry=248, importance=TRUE)

Visualisez le modèle et la table de confusion obtenue sur les échantillons OOB.

rf.fit


Call:
 randomForest(formula = cancer.type ~ ., data = mat.app, ntree = ntree.opt,      mtry = 248, importance = TRUE) 
               Type of random forest: classification
                     Number of trees: 200
No. of variables tried at each split: 248

        OOB estimate of  error rate: 18.35%
Confusion matrix:
             Luminal.A no.Luminal.A class.error
Luminal.A          252           28   0.1000000
no.Luminal.A        59          135   0.3041237

Calcul des performances du modèle random forest

Pour comparer les performances de ce modèle, avec le modèle CART calculé précédemment, il faut calculer l’accuracy du modèle rf.fit sur les données des échantillons d’apprentissage et de test.

Calculez l’accuracy du modèle sur les données de l’apprentissage

# Prédiction du type de cancer des individus du jeu d'apprentissage
pred.app <- predict(rf.fit, newdata = mat.app, type="class")

# matrice de confusion entre les données prédites sur l'échantillon d'apprentissage et les vraies valeurs.

tc.rf.app <- table(pred.app, mat.app[,"cancer.type"])
tc.rf.app

              
pred.app       Luminal.A no.Luminal.A
  Luminal.A          280            0
  no.Luminal.A         0          194

#  accuracy* du modèle sur les données de l'apprentissage
acc.rf.app <- sum(diag(tc.rf.app))/sum(tc.rf.app)
acc.rf.app

[1] 1

Calcul de l’accuracy sur l’échantillon test

# prediction
pred.test <- predict(rf.fit, newdata = mat.test, type="class")

# table de confusionr.fit
tc.rf.test <- table(pred.test, mat.test[,"cancer.type"])
tc.rf.test

              
pred.test      Luminal.A no.Luminal.A
  Luminal.A          126           30
  no.Luminal.A        16           66

#accuracy
acc.rf.test <- sum(diag(tc.rf.test))/sum(tc.rf.test)
acc.rf.test

[1] 0.8067227

Comparez les performances des modèles de CART et de Random forest.
Etude de l’importance des variables (ici les gènes) dans le modèle.

Représentez graphiquement l’importance de chaque gène en utilisant la fonction varImpPlot()

varImpPlot(rf.fit, n.var=50, cex = 0.7, type=1)

Identifiez les gènes qui permettent de différentier le cancer Luminal.A des autres cancers.
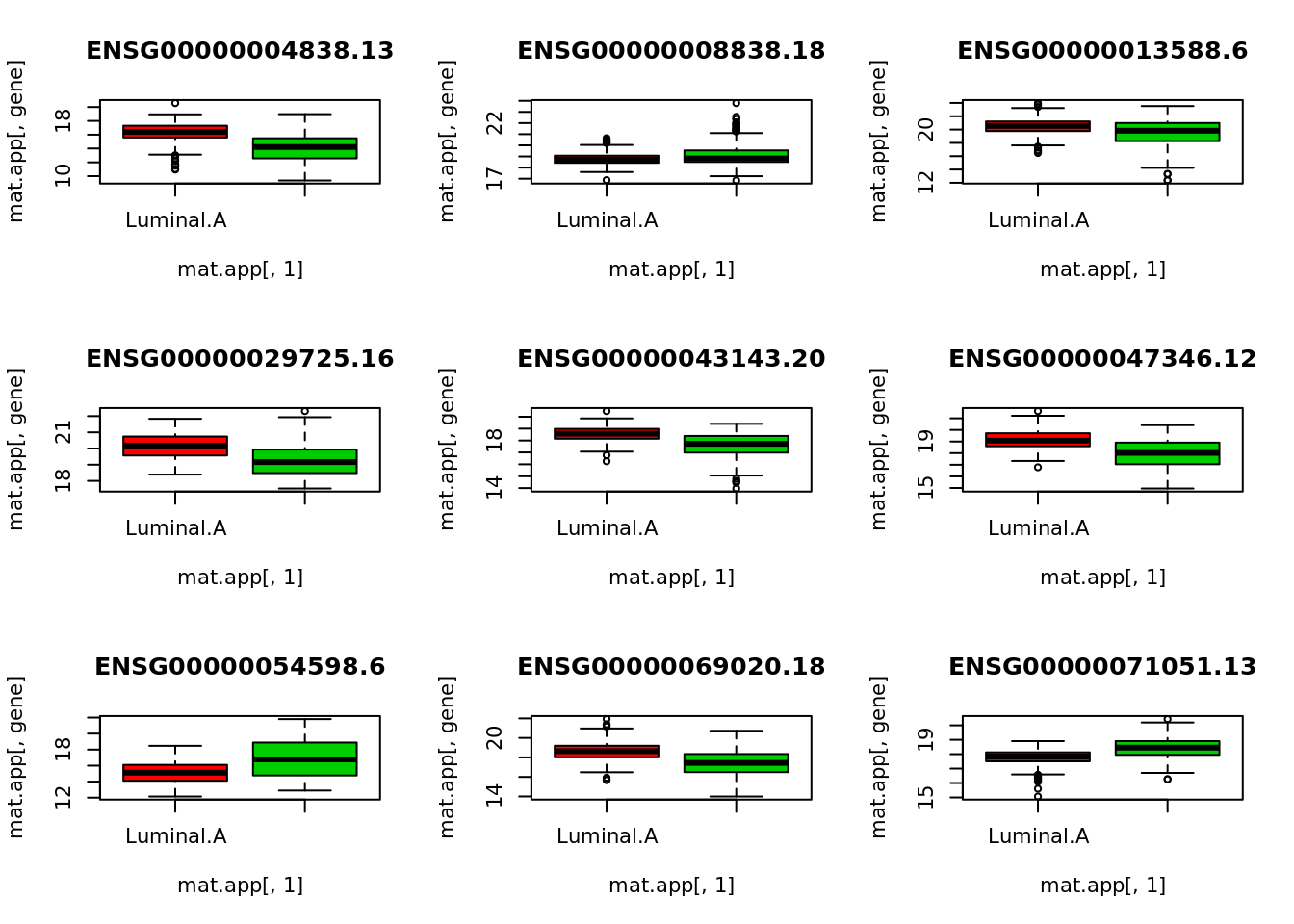
Pour chaque gene sélectionné, tracez la distribution de l’expression du gène chez les patients atteints d’un cancer de type Luminal.A et chez les autres patients d’après les données d’apprentissage.

v.imp <- importance(rf.fit)[,"MeanDecreaseAccuracy"]
gene.sel <- names(which(v.imp>4))

par(mfrow=c(3,3))
for(gene in gene.sel){
  boxplot(mat.app[,gene]~mat.app[,1],col=c(2,3), main=gene)
}

Représentez la matrice des données en focalisant sur les gènes sélectionnées et en utilisant une heatmap.

#Trier les individus par type de cancer
ind.app.lA <- which(mat.app[,"cancer.type"]=="Luminal.A")
ind.tri <- c(ind.app.lA, setdiff(1:nrow(mat.app), ind.app.lA))
mat.app.tri <- t(mat.app[ind.tri, gene.sel])

# Compute mean value per gene
gene.means <- apply(mat.app.tri, 1, mean)
gene.sd <-  apply(mat.app.tri, 1, sd)

# Compute gene-wise centered expression values
BIC.expr.genes.centered <- mat.app.tri - gene.means

# Compute gene-wise centred + scaled expression values
BIC.expr.genes.standardized <- BIC.expr.genes.centered / gene.sd

## define a Blue - White - Red palette
frenchflag.palette <- colorRampPalette(c('dark blue','white','dark red'))

## Define a green - black - red palette
GBR.palette <- colorRampPalette(c('green','black','red'))

heatmap(as.matrix(BIC.expr.genes.standardized),
        zlim = c(-4,4), Colv=NA,
        distfun = function(x) as.dist(1 - cor(t(x), method = "spearman")), 
        hclustfun = function(x) hclust(x, method = "ward.D2"),
        labRow = NA, labCol = NA,  # DO not print the labels (unreadable anyway)
        col = GBR.palette(100),
        scale = "none")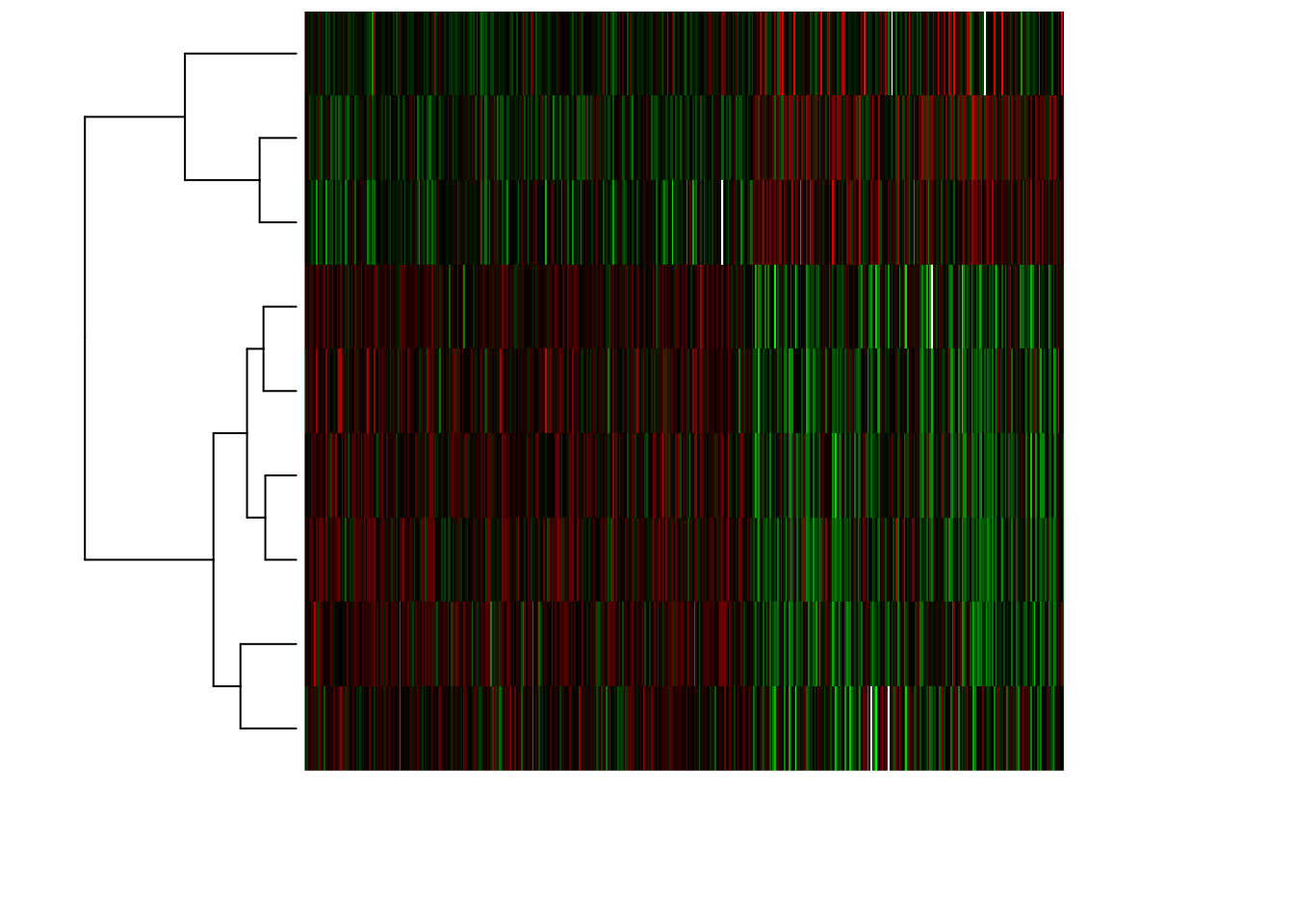

6 Prédiction du type de cancer en utilisant les Support Vecteur Machines

utilisation avec formule R

library(e1071)
model=svm(cancer.type ~ ., data = mat.app)

utilisation classique

X=subset(mat.app, select = -cancer.type)
y=mat.app$cancer.type
model=svm(X,y)

erreur d’apprentissage avec les paramètres par défaut

pred=predict(model, X)
table(pred, mat.app$cancer.type)

surapprentissage avec gaussiennes très resserrées

model=svm(X,y,gamma=0.1)
pred=predict(model, X)
table(pred, mat.app$cancer.type)

surapprentissage avec cost élevé

model=svm(X,y,cost=100)
pred=predict(model, X)
table(pred, mat.app$cancer.type)

évaluation d’erreur de test (en surapprentissage)

Xtest=subset(mat.test, select = -cancer.type)
pred=predict(model, Xtest)
table(pred, mat.test$cancer.type)

évaluation d’erreur de test (avec paramètres par défaut)

model=svm(X,y)
pred=predict(model, Xtest)
table(pred, mat.test$cancer.type)

7 Prédiction des échantillons classés comme “Unclassified”

Lors de l’étude du jeu de données initial, vous avez déterminé que 107 échantillons avaient été classés comme “Unclassified”. En utilisant les modèles de random forest et de SVM, prédisez le type de cancer pour ces individus. Comparez les résultats obtenus avec les deux modèles.

Prédiction du type de cancer en utilisant le modèle random forest

mat.pred <- t(BIC.expr)
pred.uncl.rf <- predict(rf.fit, newdata = mat.pred[ind.uncl,])
table(pred.uncl.rf)

pred.uncl.rf
   Luminal.A no.Luminal.A 
          54           53

Prédiction du type de cancer en utilisant le modèle SVM

model=svm(cancer.type~., data=mat.app)
pred.uncl.svm <- predict(model, newdata = mat.pred[ind.uncl,])
table(pred.uncl.svm)

pred.uncl.svm
   Luminal.A no.Luminal.A 
          67           40

Calcul de la table de confusion entre les deux vecteurs de prédiction

tc <- table(pred.uncl.rf, pred.uncl.svm)
tc

              pred.uncl.svm
pred.uncl.rf   Luminal.A no.Luminal.A
  Luminal.A           54            0
  no.Luminal.A        13           40

8 Prédiction des 4 types de cancer

Préparation du jeu de données

Créez un nouveau data.frame (df.data.4) qui contient les données d’expression de gènes contenu dans le data.frame BIC.expr.4 et le type de cancer pour chaque échantillon (définit en 4 types).

df.data.4 <- data.frame(as.character(BIC.sample.classes.4[,1]), t(BIC.expr.4))
df.data.4[,1] <- as.factor(df.data.4[,1])
colnames(df.data.4)[1] <- "cancer.type"

Préparation des échantillons d’apprentissage et de test

En reprenant les individus sélectionnés pour la création de l’échantillon d’apprentissage ind.app, créez les data.frames mat.app.4 et mat.test.4 qui contiennent les données de l’échantillon d’apprentissage et celui de test.

mat.app.4 <- df.data.4[ind.app,]
dim(mat.app.4)

[1] 474 965

Préparez l’échantillon test

mat.test.4 <- df.data.4[-ind.app,]
dim(mat.test.4)

[1] 238 965

Déterminez les paramètres mtry et ntree optimaux pour le random forest permettant de prédire les 4 types de cancer.

Déterminez la valeur optimale du paramètre ntree

rf.fit.4 <- randomForest(cancer.type~., data=mat.app.4)
plot(rf.fit.4$err.rate[,1], type="l", ylab = "taux d'erreur", xlab="nombre d'arbres")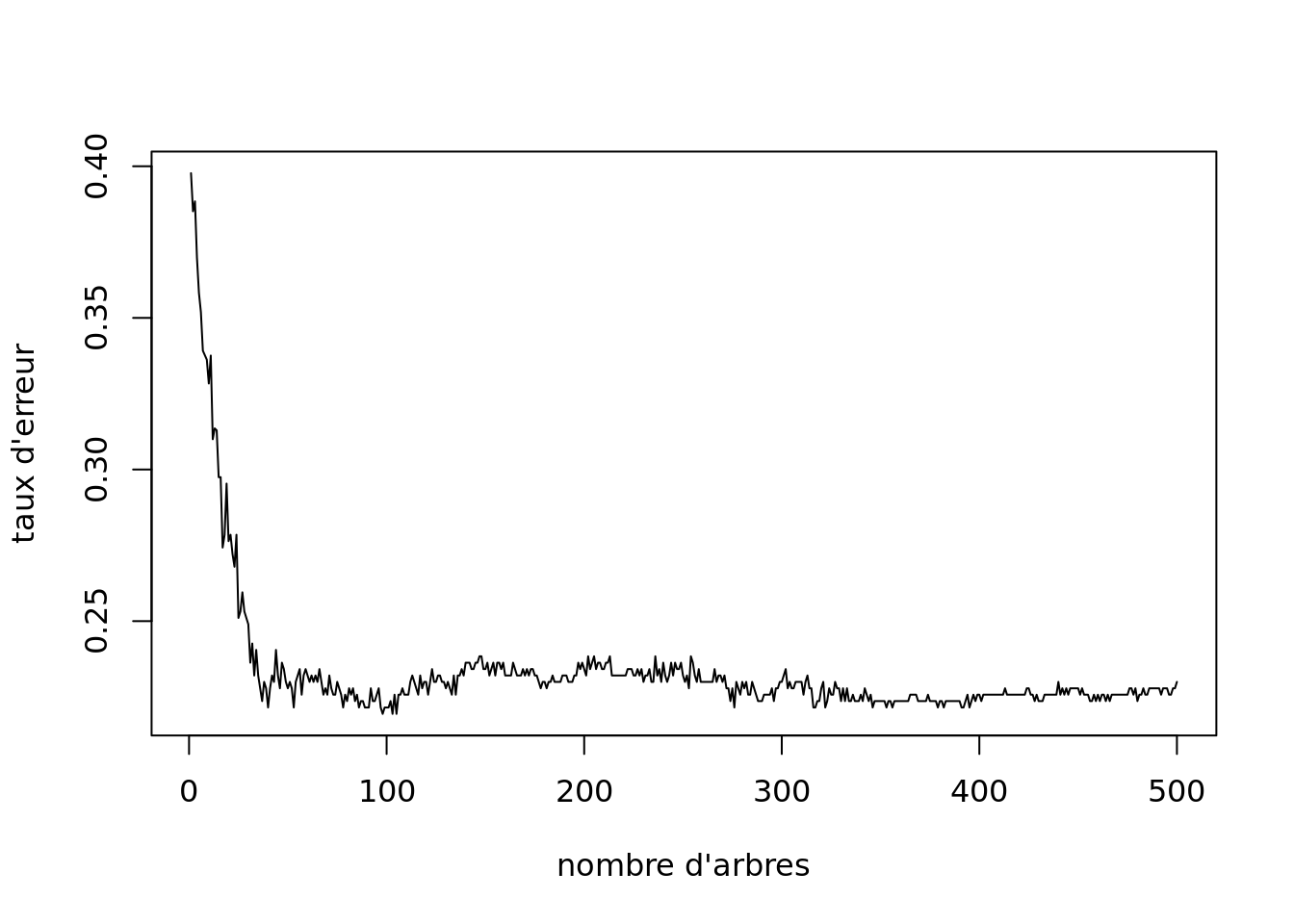

Déterminez la valeur optimale du paramètre mtry.

v.err <-  NULL
v.mtry <- c(15, 31, 62, 124, 248, 350, 500)
for(i in v.mtry){
    set.seed(123)
    rf.fit <- randomForest(cancer.type~., data = mat.app.4, ntree=150, mtry=i)
    v.err <- c(v.err, rf.fit$err.rate[150,1])
}

plot(v.mtry, v.err, type ="b", xlab="mtry values", ylab="taux d'erreur", xaxt="n")
axis(1, at=v.mtry, labels=v.mtry, las=2)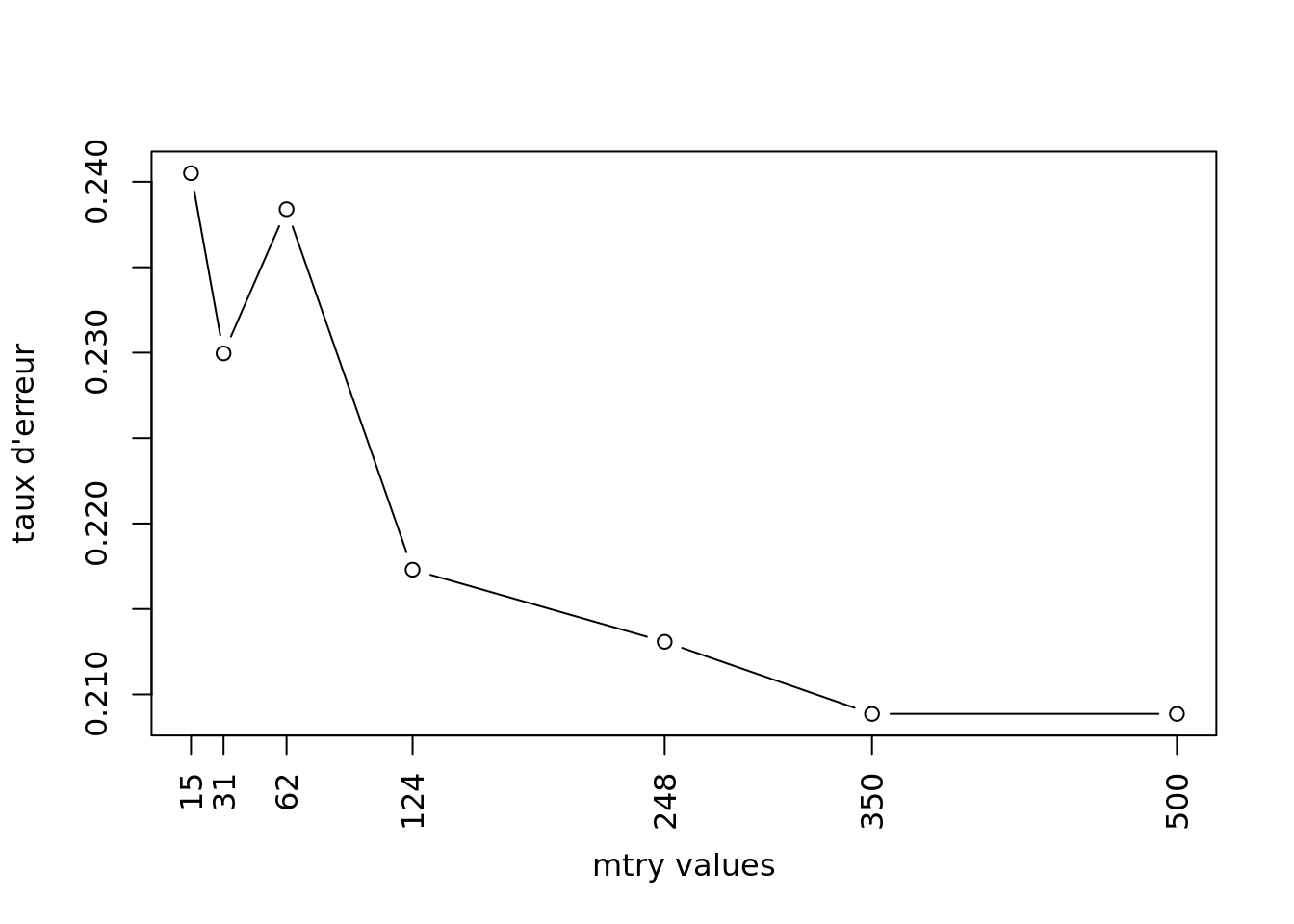

Calculez le modèle avec les paramètres optimaux.
Calculez à nouveau le modèle sur l’échantillon d’apprentissage en utilisant les valeurs optimales des paramètres mtry et ntree. Dans la fonction randomForest(), ajouter l’argument importance=TRUE.

rf.fit.4 <- randomForest(cancer.type~., data = mat.app.4, ntree=150, mtry=124, importance=TRUE)

Visualisez le modèle et la table de confusion obtenue sur les échantillons OOB.

rf.fit.4


Call:
 randomForest(formula = cancer.type ~ ., data = mat.app.4, ntree = 150,      mtry = 124, importance = TRUE) 
               Type of random forest: classification
                     Number of trees: 150
No. of variables tried at each split: 124

        OOB estimate of  error rate: 22.57%
Confusion matrix:
           Basal.like HER2pos Luminal.A Luminal.B class.error
Basal.like         75       0        14         0  0.15730337
HER2pos             5       6        11         8  0.80000000
Luminal.A           3       0       274         3  0.02142857
Luminal.B           0       0        63        12  0.84000000

Calculez les performances du modèle random forest sur l’échantillon d’apprentissage et de test.

Calcul de l’accuracy sur l’échantillon d’apprentissage.

pred.app.4 <- predict(rf.fit.4, newdata = mat.app.4, type="class")
tc.rf4.app <- table(pred.app.4, mat.app.4[,"cancer.type"])
tc.rf4.app

            
pred.app.4   Basal.like HER2pos Luminal.A Luminal.B
  Basal.like         89       0         0         0
  HER2pos             0      30         0         0
  Luminal.A           0       0       280         0
  Luminal.B           0       0         0        75

acc.rf4.app <- sum(diag(tc.rf4.app))/sum(tc.rf4.app)
acc.rf4.app

[1] 1

Calcul de l’accuracy sur l’échantillon test

pred.test.4 <- predict(rf.fit.4, newdata = mat.test.4, type="class")

tc.rf4.test <- table(pred.test.4, mat.test.4[,"cancer.type"])
tc.rf4.test

            
pred.test.4  Basal.like HER2pos Luminal.A Luminal.B
  Basal.like         31       4         2         1
  HER2pos             3       2         0         0
  Luminal.A           8       2       139        34
  Luminal.B           0       3         1         8

acc.rf4.test <- sum(diag(tc.rf4.test))/sum(tc.rf4.test)
acc.rf4.test

[1] 0.7563025

Etude de l’importance des descripteurs dans le modèle.

Représentez graphiquement la valeur d’importance des différents gènes en utilisant la fonction varImpPlot()

varImpPlot(rf.fit.4, n.var=50, cex = 0.6, type=1)

Module 3 - Analyse statistique avec R - Séance 7

DUBii 2020

Leslie REGAD and Frédéric GUYON (Université Paris Diderot), adapted by Jacques va Helden and Olivier Sand

2020-07-08