Les données dans l’ordinateur (1)
Les iris de Fisher
Ces données sont un classique des méthodes d’apprentissage Fisher

Anne Badel, Frédéric Guyon & Jacques van Helden
2020-06-02
Comment découvrir des “clusters” dans les données ?
Comment comparer deux classifications ?
Ces données sont un classique des méthodes d’apprentissage Fisher

Sepal.Length Sepal.Width Petal.Length Petal.Width
1 5.1 3.5 1.4 0.2
2 4.9 3.0 1.4 0.2
3 4.7 3.2 1.3 0.2
4 4.6 3.1 1.5 0.2
5 5.0 3.6 1.4 0.2
6 5.4 3.9 1.7 0.4 Sepal.Length Sepal.Width Petal.Length Petal.Width
1 5.1 3.5 1.4 0.2
2 4.9 3.0 1.4 0.2
3 4.7 3.2 1.3 0.2
4 4.6 3.1 1.5 0.2
5 5.0 3.6 1.4 0.2
6 5.4 3.9 1.7 0.41 ligne = 1 fleur = 1 individu = 1 vecteur
1 colonne = 1 variable = 1 feature = 1 vecteur
l’ensemble des données = 1 échantillon = 1 data.frame
! : convention différente en RNA-seq
Sepal.Length Sepal.Width Petal.Length Petal.Width
1 5.1 3.5 1.4 0.2
Comment représenter cette fleur ?
Dans quel espace de réprésentation ?
Dans le plan, un point de coordonnées : \(x = 5.1\), \(y = 3.5\)
représenté par un vecteur \(v2 = (5.1, 3.5)\) dans \(\mathbb{R}^2\)
Dans l’espace, un point de coordonnées :
représenté par un vecteur \(v3 = (\) 5.1 \(,\) 3.5 \(,\) 1.4\()\) dans \(\mathbb{R}^3\)
= un nuage de points dans un espace à 4 dimensions
= PAS de représentation possible (pour l’instant)
c’est à dire de toutes les variables à notre disposition
On a une information sur nos données
Clustering : on cherche à mettre en évidence des groupes dans les données
On a une information sur nos données
Clustering : on cherche à mettre en évidence des groupes dans les données
Classification :
on connaît le partitionnement de notre jeu de données
la classification appartient aux méthodes dites supervisées, ou prédictives
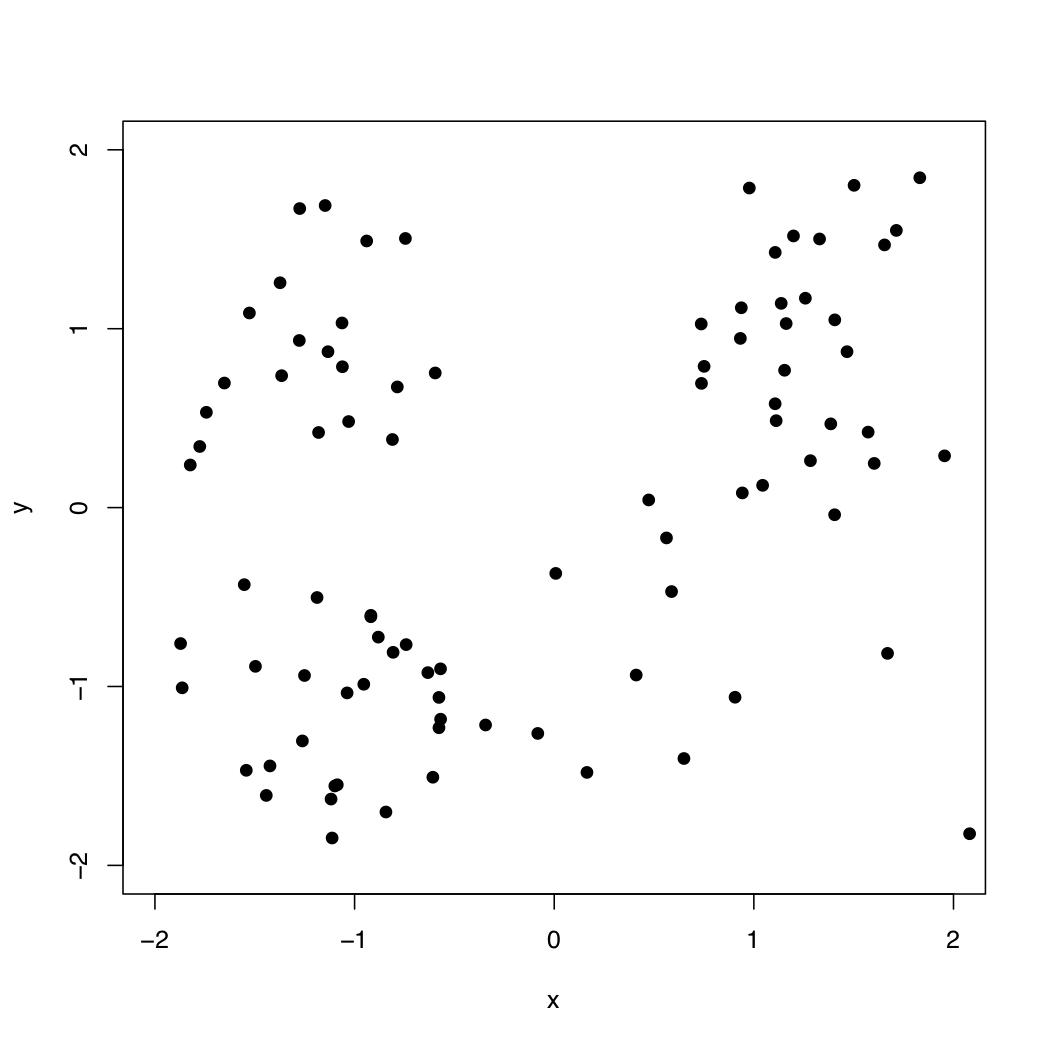
données simulées : y a-t-il des groupes ?
On considère les données comme des points de \(\mathbb{R}^n\)
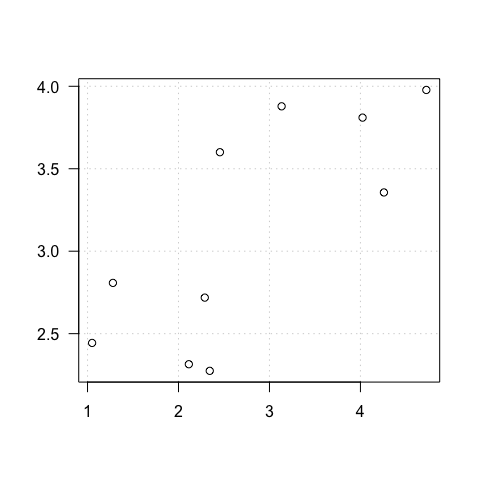
\(\mathbb{R}^n\) : espace Euclidien à \(n\) dimensions, où
On considère les données comme des points de \(R^n\) (*)
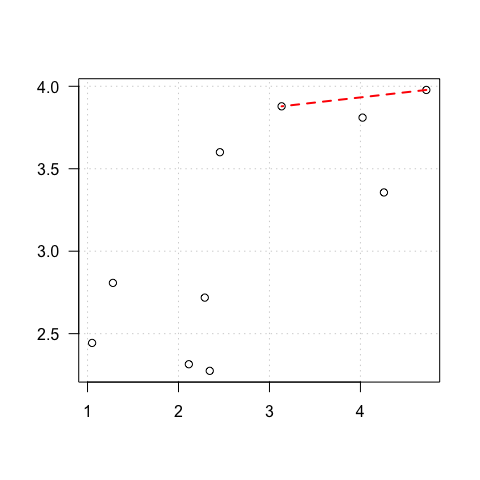
Sur la base d’une distance (souvent euclidienne)
Clustering :
Définition d’une distance : fonction positive de deux variables
Si 1,2,3 : dissimilarité
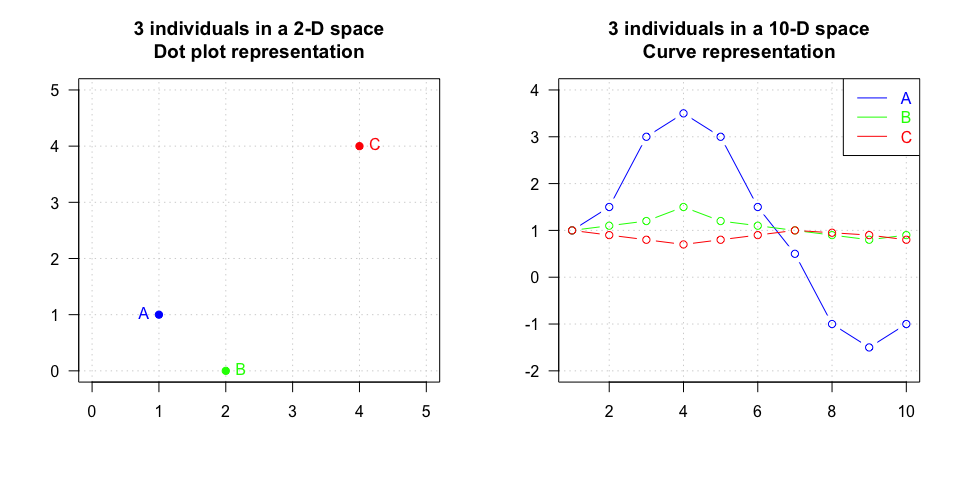
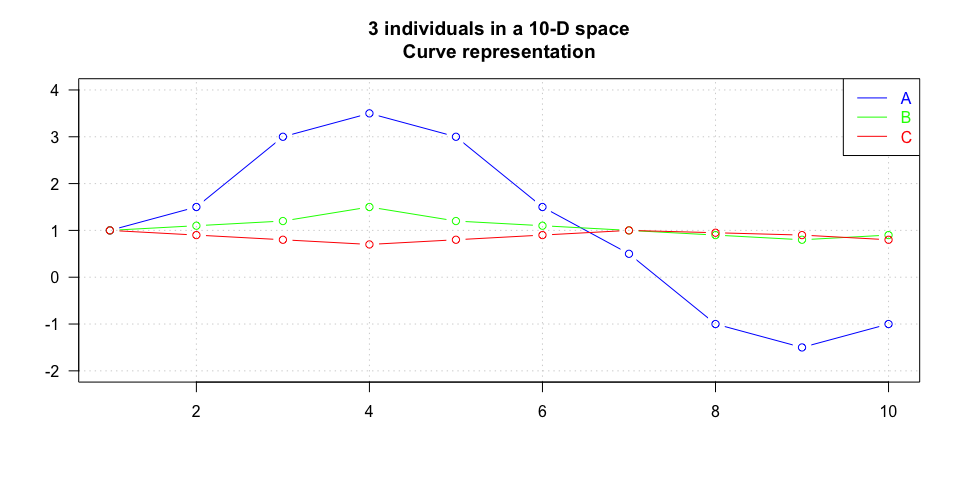
| distance euclidienne | coefficient de corrélation | distance de corrélation | |
|---|---|---|---|
| A - B | 4.85 | 0.93 | 0.07 |
| A - C | 5.59 | -0.53 | 1.53 |
| B - C | 1.03 | -0.67 | 1.67 |
on utilise la fonction dist() avec l’option method = "euclidean", "manhattan", ...
| t1 | t2 | t3 | t4 | t5 | SUM | |
|---|---|---|---|---|---|---|
| X | 1.28 | 4.72 | 1.05 | 3.13 | 4.26 | 14.45 |
| Y | 2.81 | 3.98 | 2.44 | 3.88 | 3.36 | 16.46 |
| abs(Y - X) | 1.53 | 0.75 | 1.39 | 0.75 | 0.90 | 5.32 |
| (Y - X)^2 | 2.34 | 0.56 | 1.94 | 0.56 | 0.81 | 6.20 |
| Eucl | 1.53 | 0.75 | 1.39 | 0.75 | 0.90 | 2.49 |
distance euclidienne : 2.49
distance de manhattan = 5.32
45 5 115 17
5 0.58
115 3.97 4.45
17 0.68 0.55 4.45
78 3.81 4.30 1.16 4.23 45 5 115 17
5 0.0025
115 0.4445 0.4800
17 0.0098 0.0024 0.5217
78 0.2811 0.3105 0.0228 0.3464 Sepal.Length Sepal.Width Petal.Length
Sepal.Width 1.723
Petal.Length 0.164 1.960
Petal.Width 0.275 1.949 0.035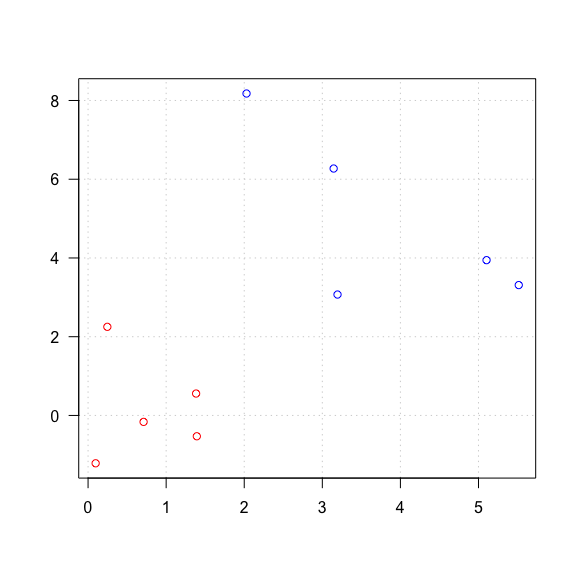
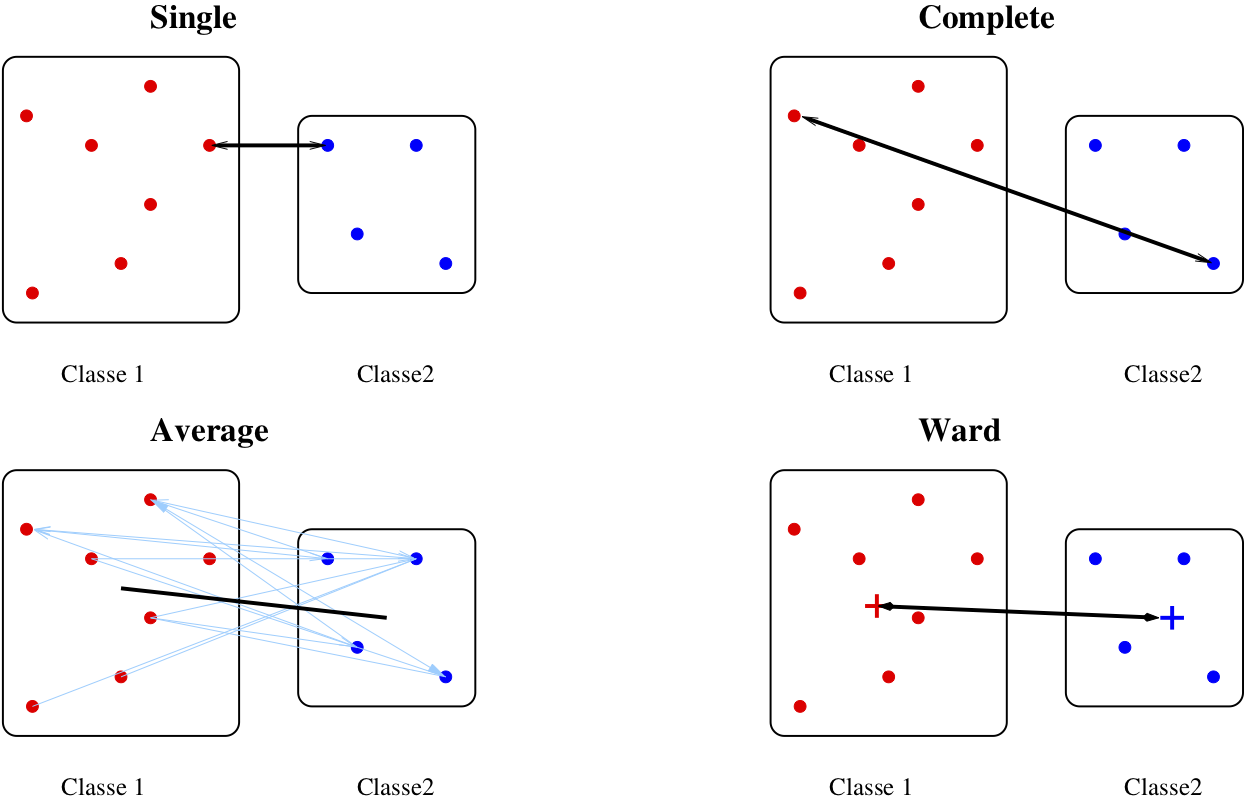
\[D(C_1,C_2) = \min_{i \in C_1, j \in C_2} D(x_i, x_j)\]
\[D(C_1,C_2) = \max_{i \in C_1, j \in C_2} D(x_i, x_j)\]
\[D(C_1,C_2) = \frac{1}{N_1 N_2} \sum_{i \in C_1, j \in C_2} D(x_i, x_j)\]
\(d^2(C_i,C_j) = I_{intra}(C_i \cup C_j)-I_{intra}(C_i)-I_{intra}(C_j)\)
\(D(C_1,C_2) = \sqrt{\frac{N_1N_2}{N_1 + N_2}} \| m_1 -m_2 \|\)
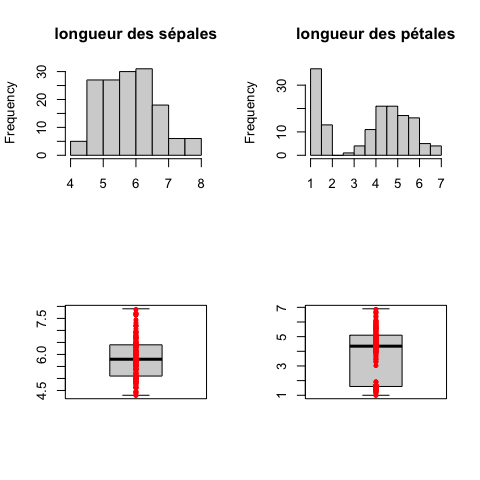
Revenons à nos iris de Fisher
On peut ensuite essayer de visualiser les données
plot (! ne pas faire si “grosses” données)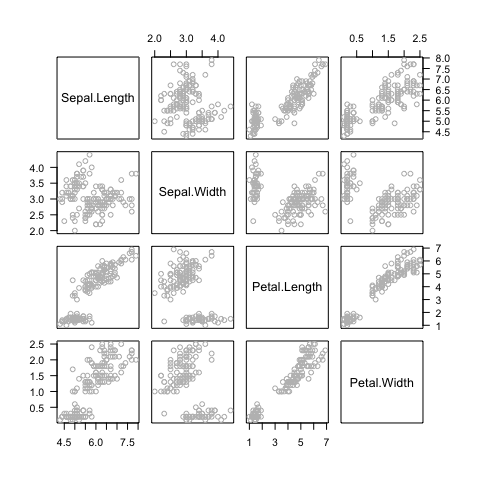
| Variance | |
|---|---|
| Sepal.Length | 0.686 |
| Sepal.Width | 0.190 |
| Petal.Length | 3.116 |
| Petal.Width | 0.581 |
[1] 0Afin de pouvoir considérer que toutes les variables sont à la même échelle, il est parfois nécessaire de standardiser les données.
soit
soit
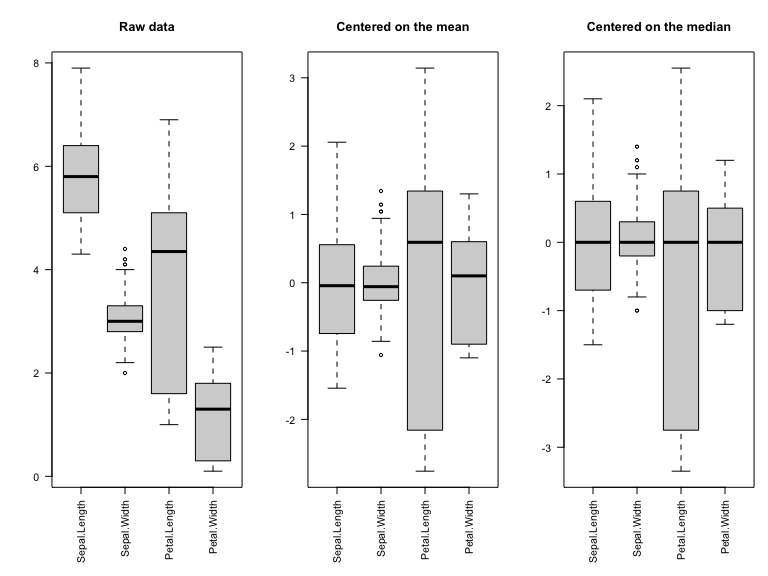
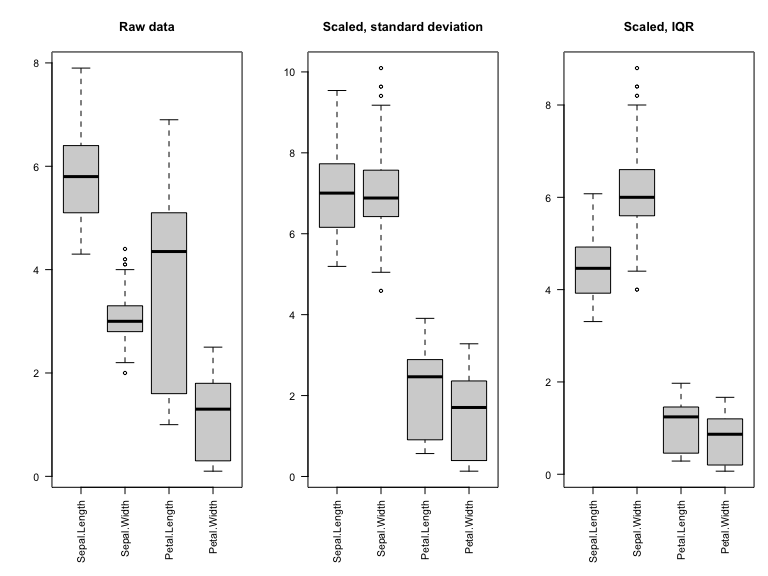
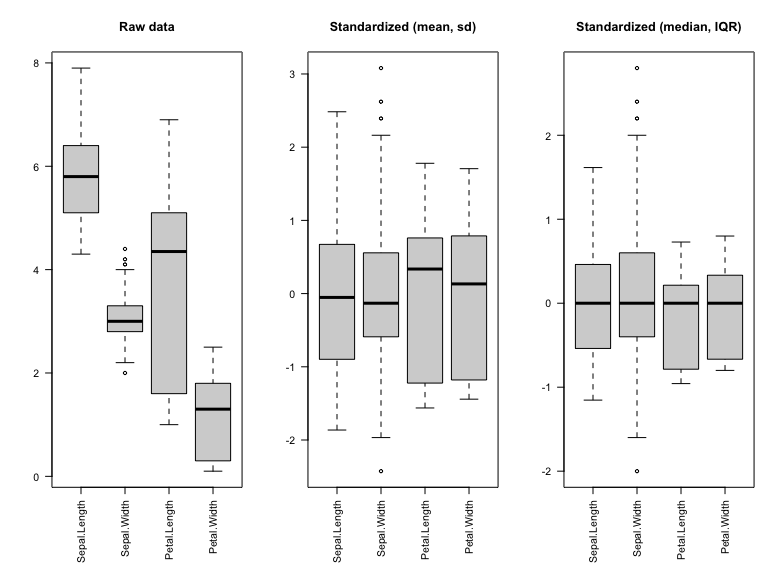
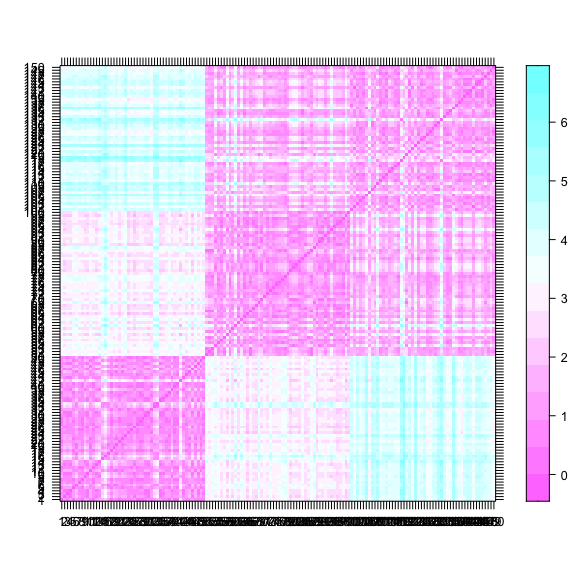
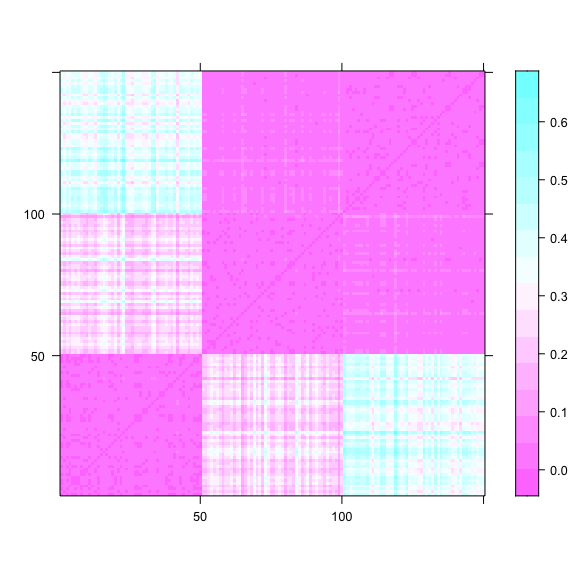
classification hiérarchique : mettre en évidence des liens hiérachiques entre les individus
ressemblance entre individus = distance
ressemblance entre groupes d’invidus = critère d’aggrégation
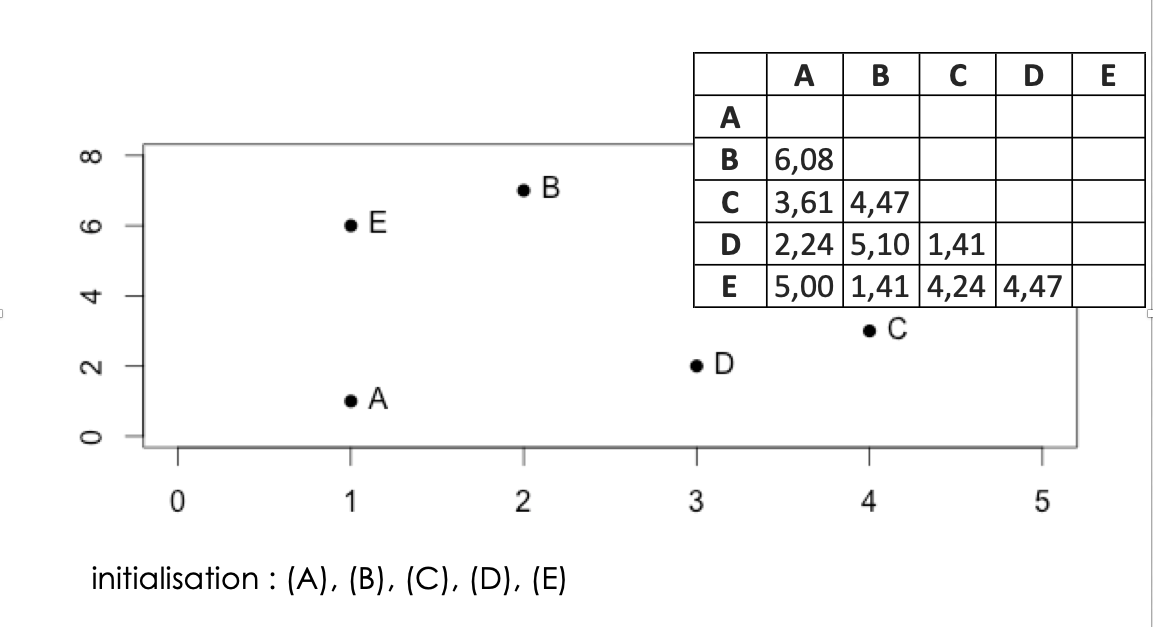
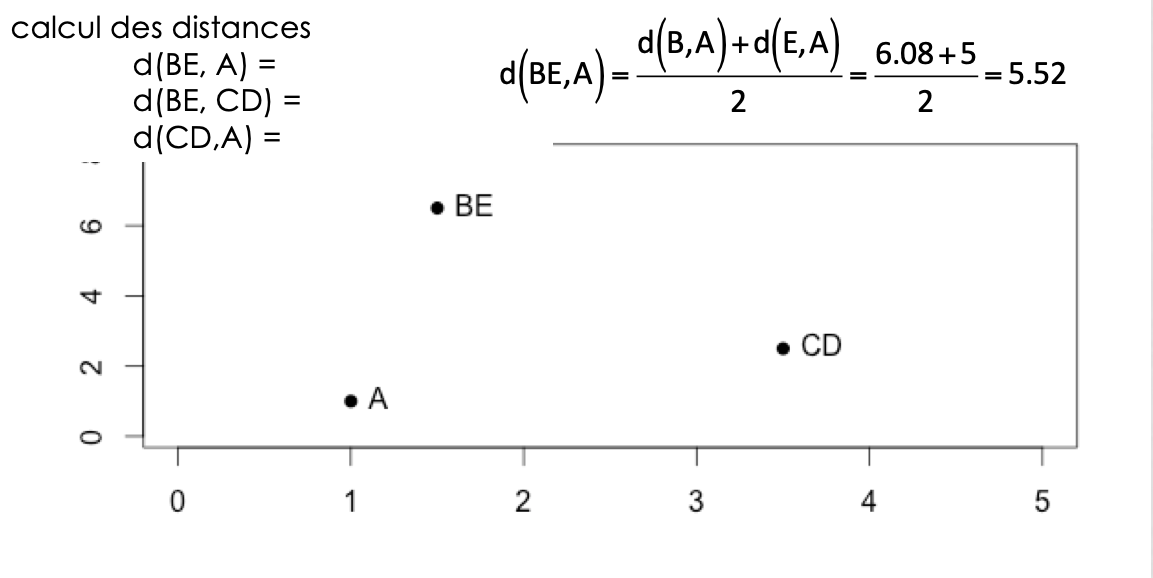
calcul des distances entre tous les individus
regroupement des 2 individus les plus proches => (n-1) clusters
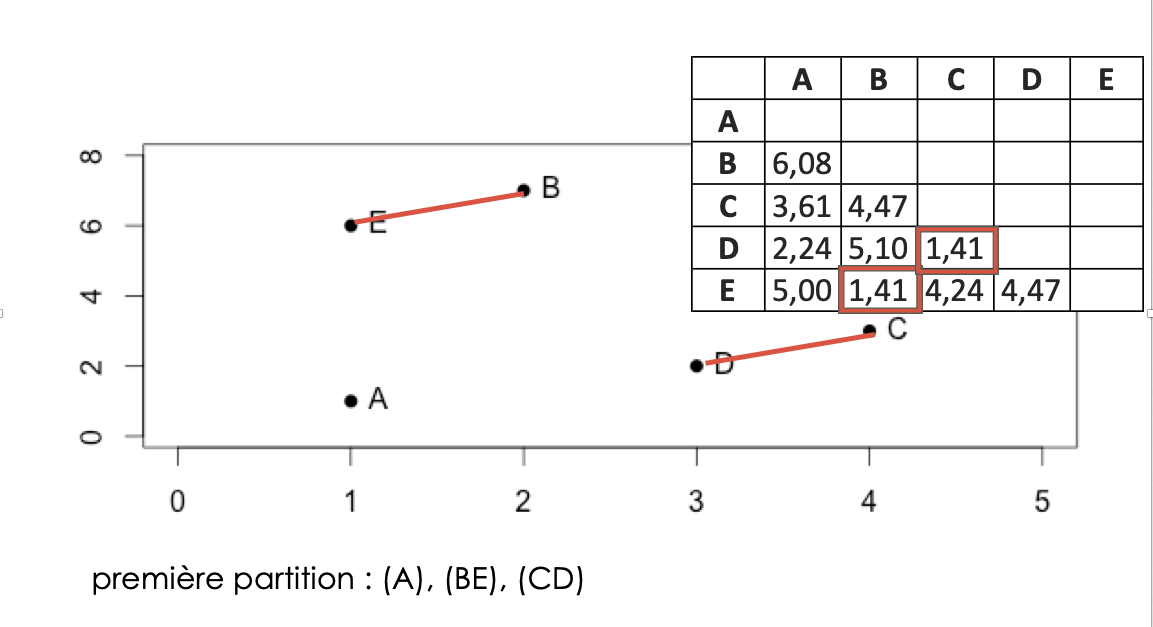

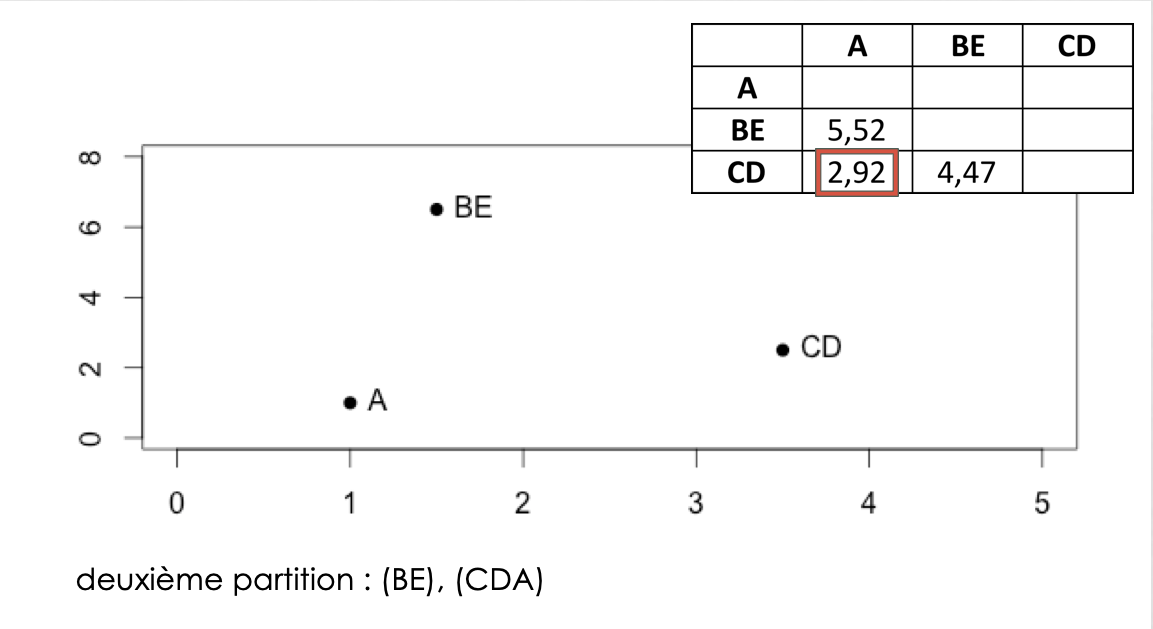
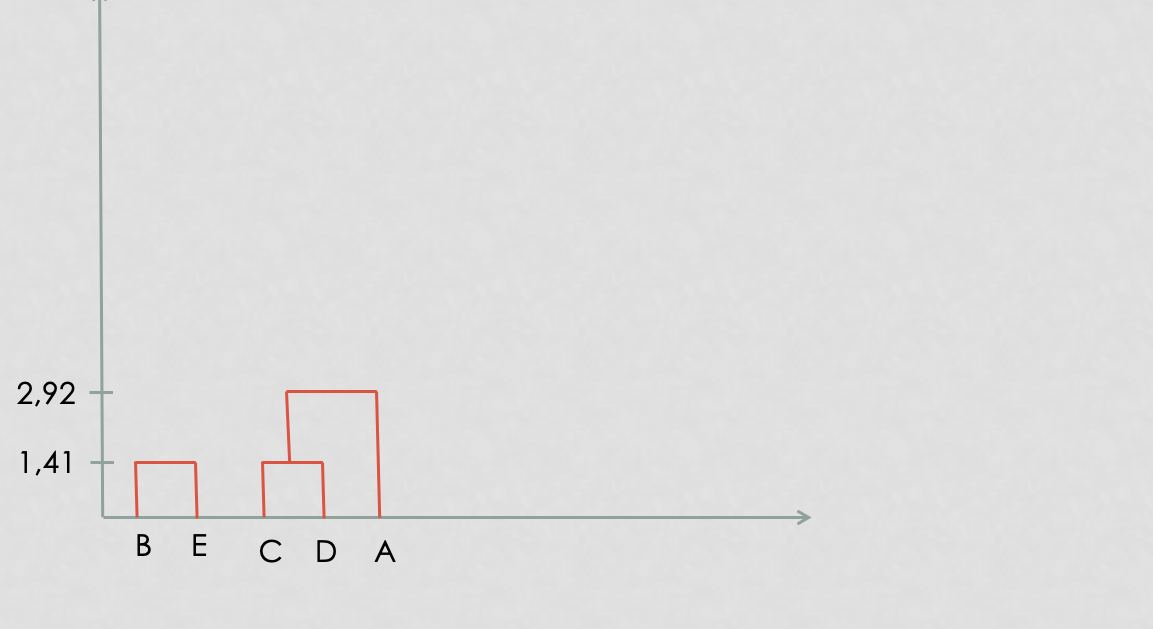
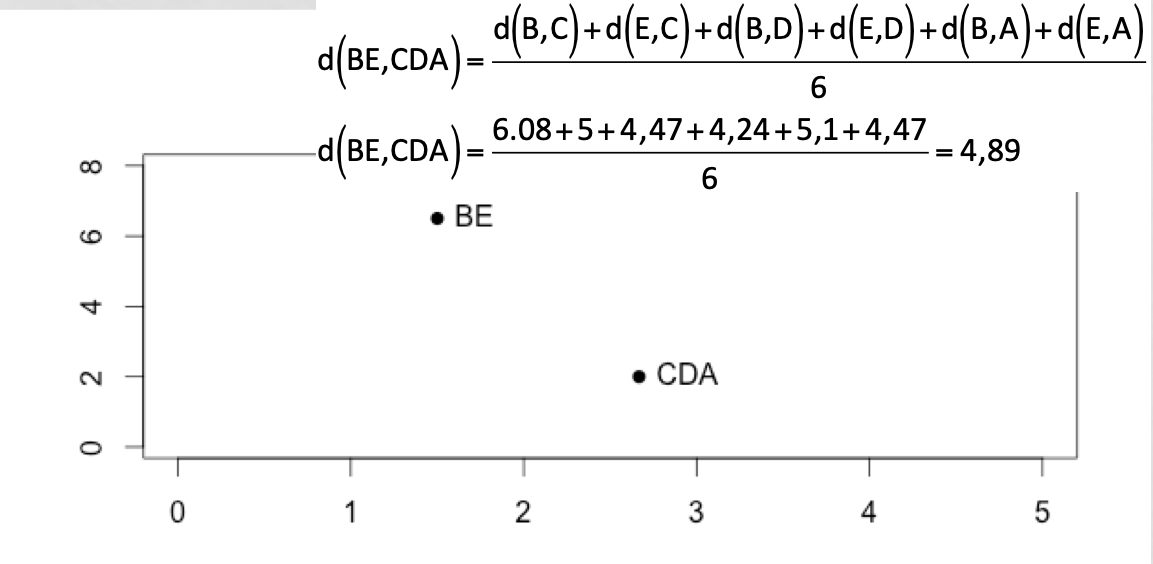
calcul des dissemblances entre chaque groupe obtenu à l’étape \((j-1)\)
regroupement des deux groupes les plus proches => \((n-j)\) clusters
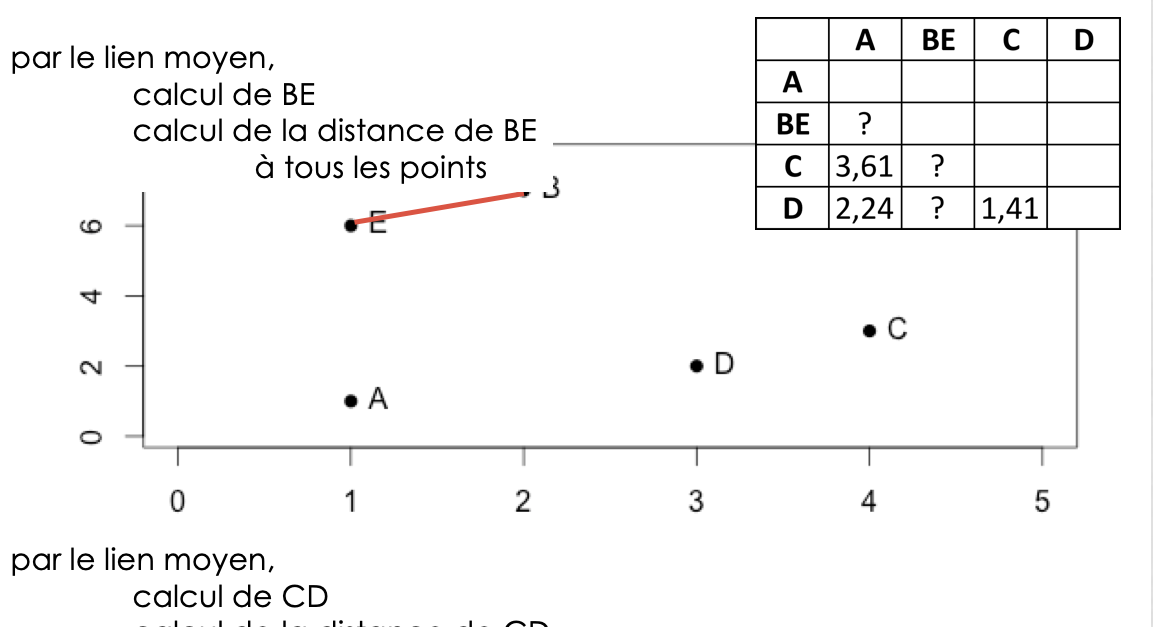
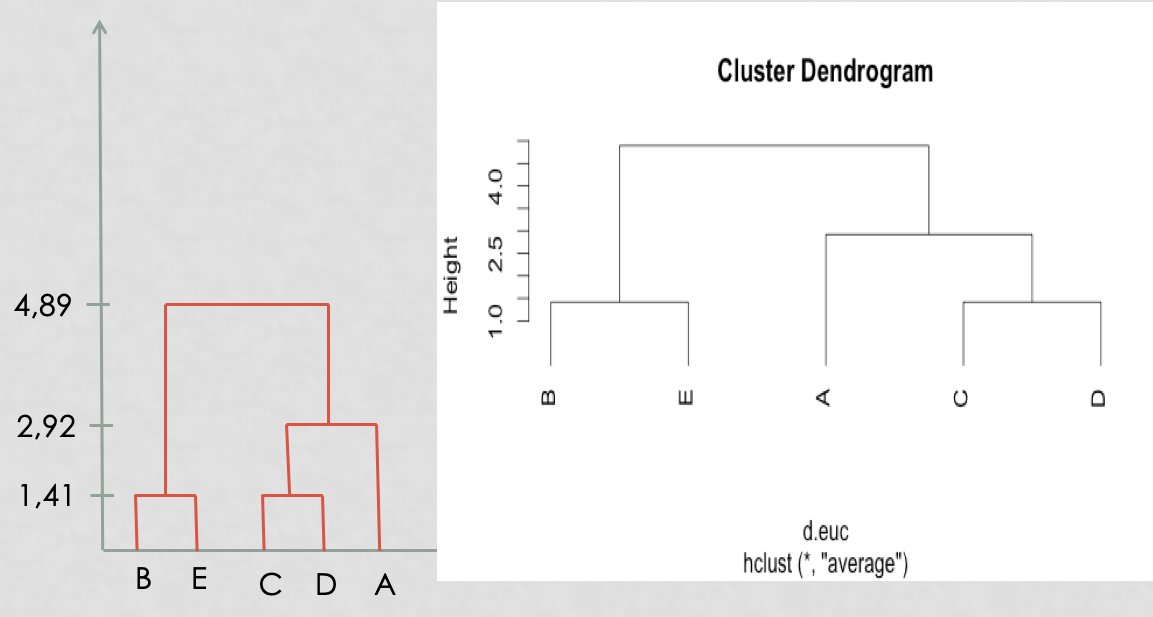
… c’est à dire aux options des fonctions dist() et hclust()
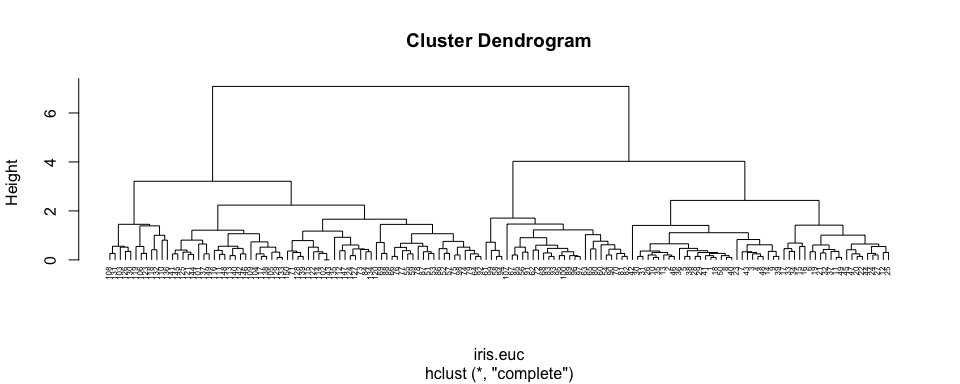
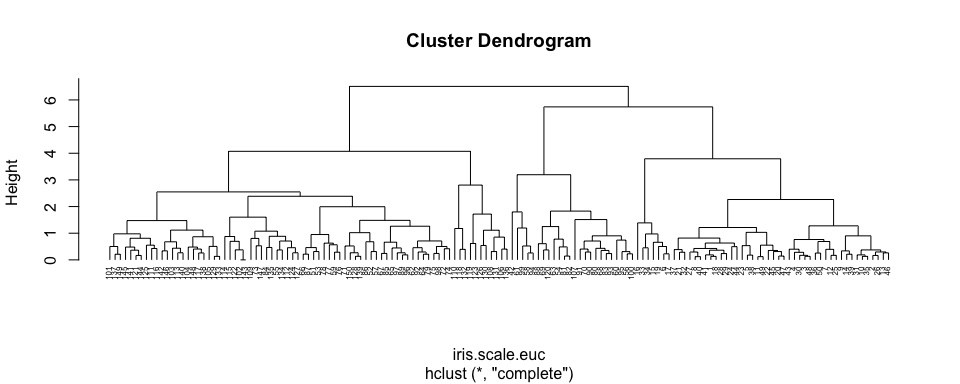
par(mfrow = c(2, 1))
plot(iris.hclust, hang = -1, cex = 0.5, main = "Données brutes")
plot(iris.scale.hclust, hang = -1, cex = 0.5, main = "Normalisées")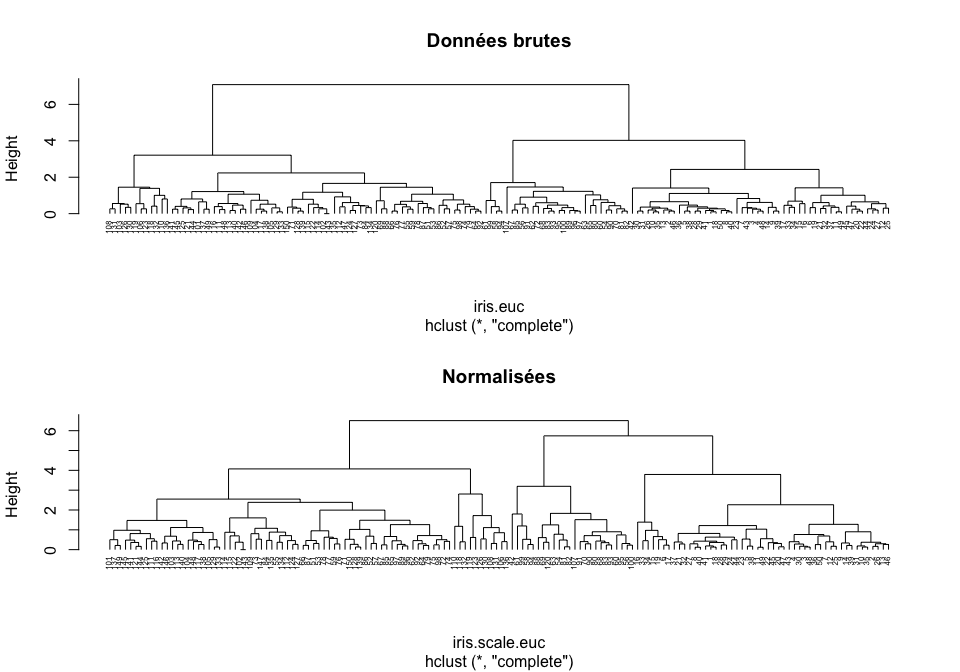
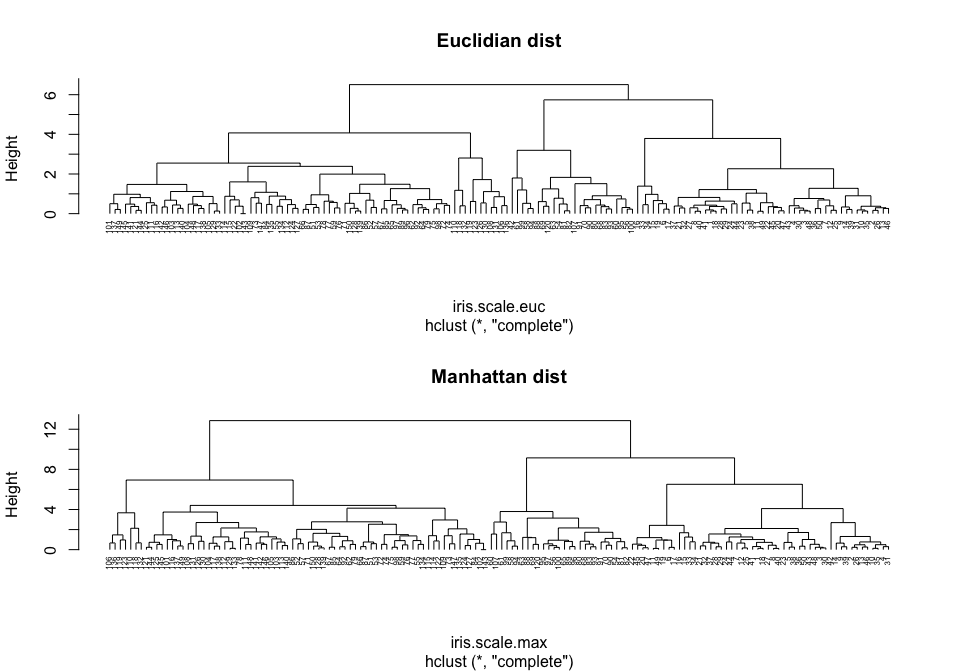
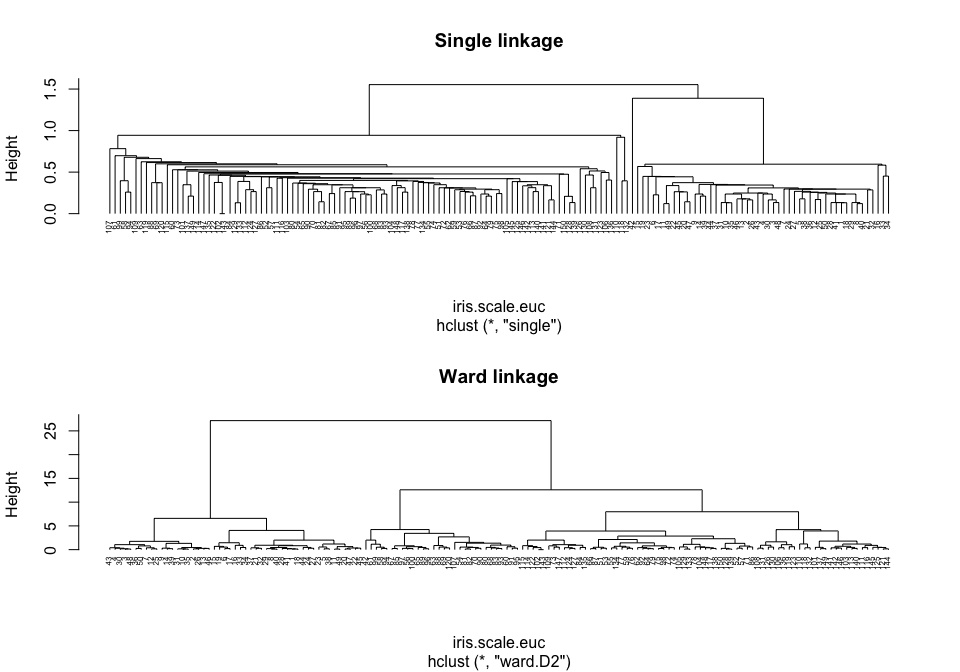
Faire attention au données
Choisir la distance et le critère d’aggrégation adaptés à nos données
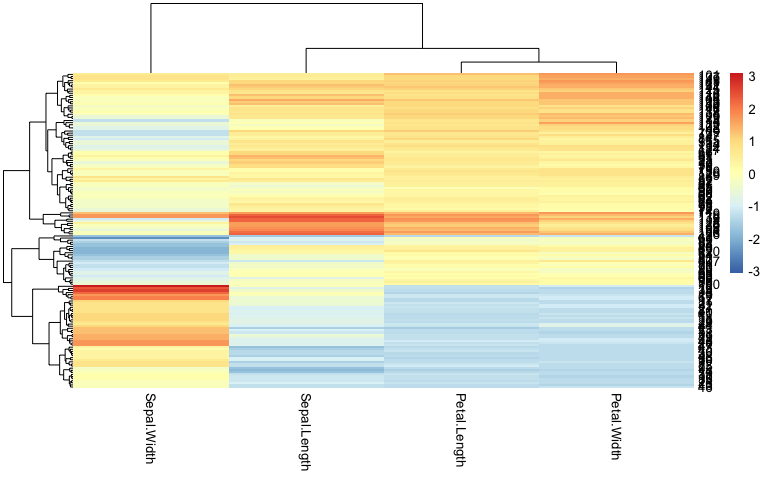
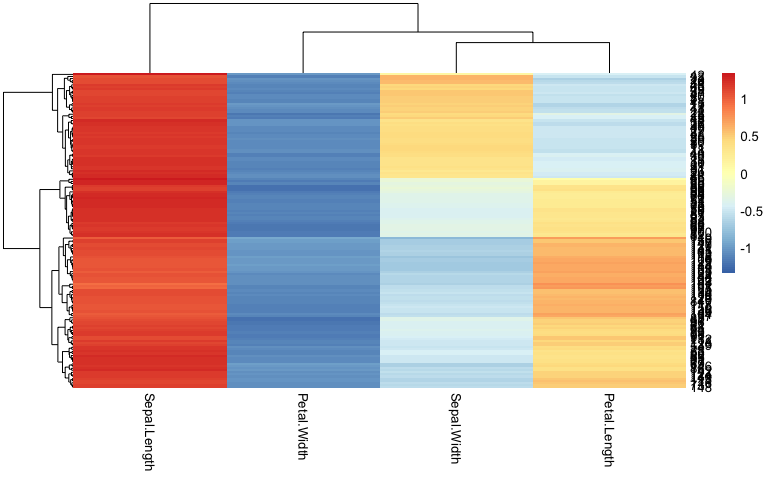
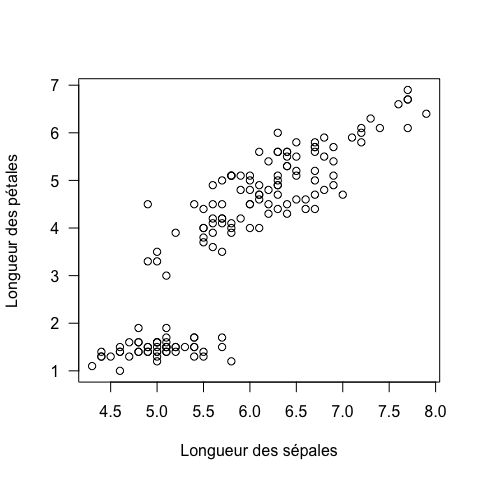
Les individus dans le plan
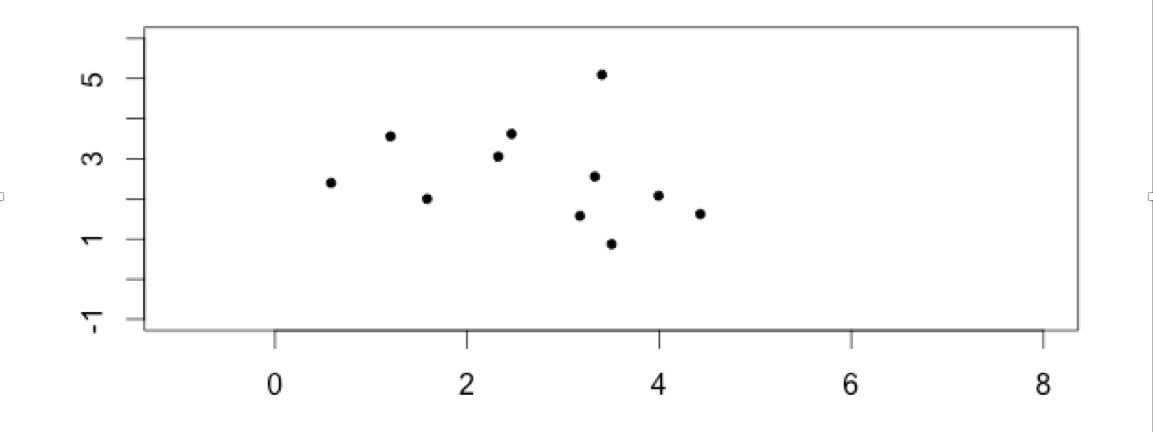
=> faire apparaitres des classes / des clusters
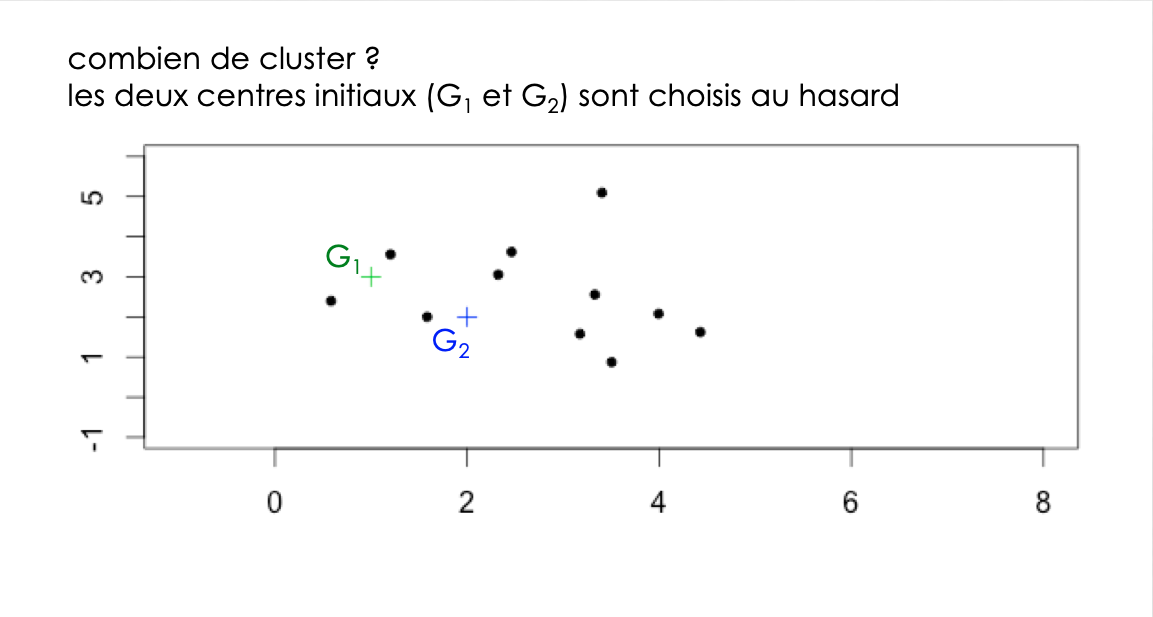
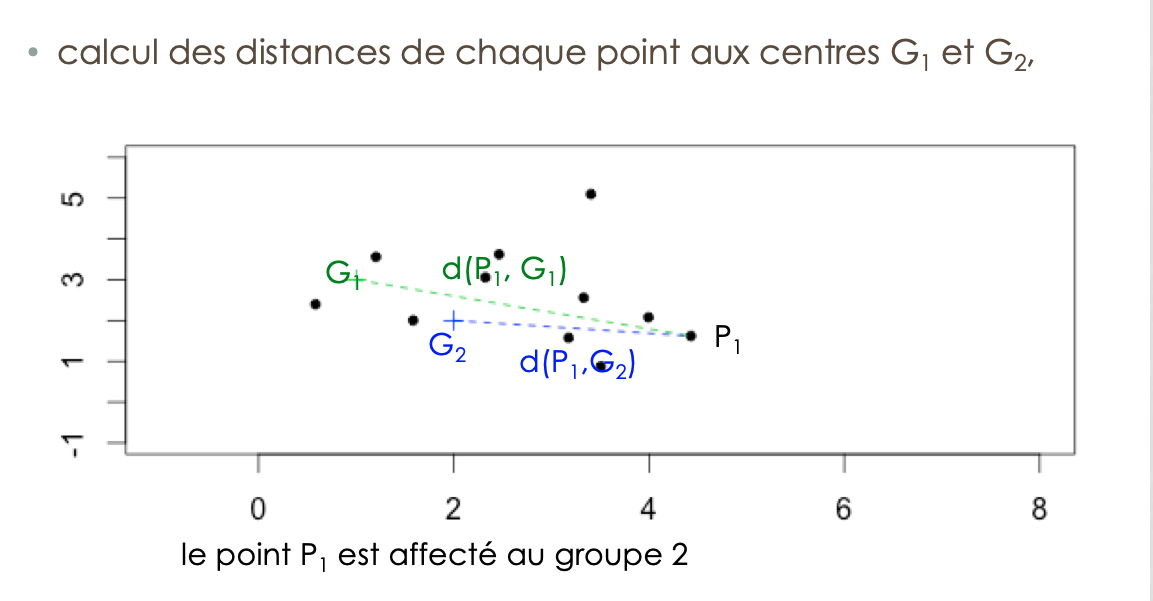
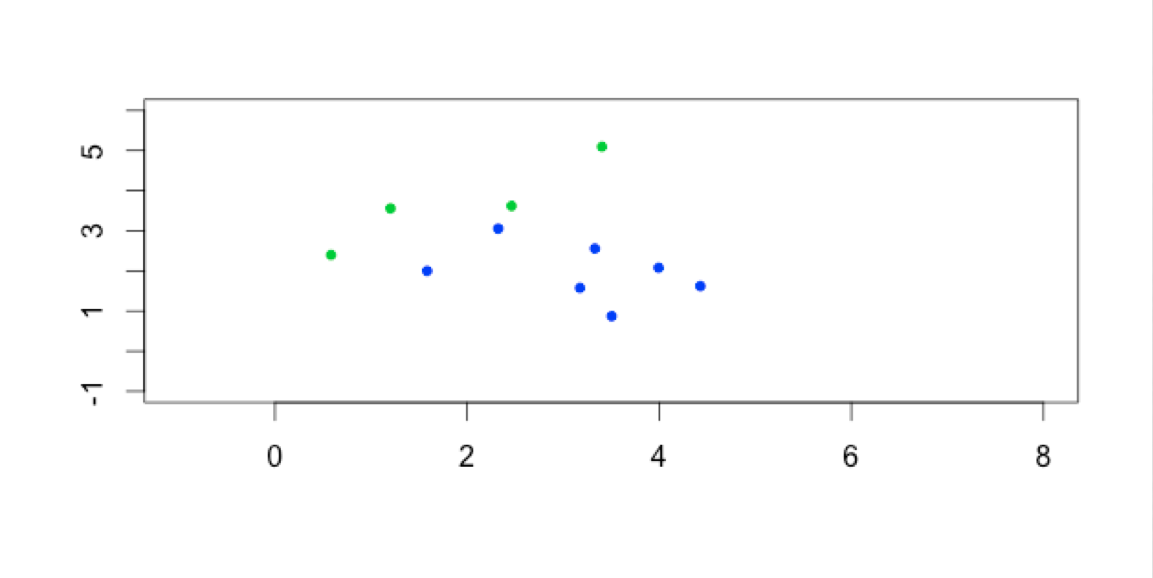
construction des centres de gravité des k clusters construits à l’étape \((j-1)\)
\(k\) nouveaux clusters créés à partir des nouveaux centres suivant la même règle qu’à l’étape \(0\)
obtention de la partition \(P_j\)
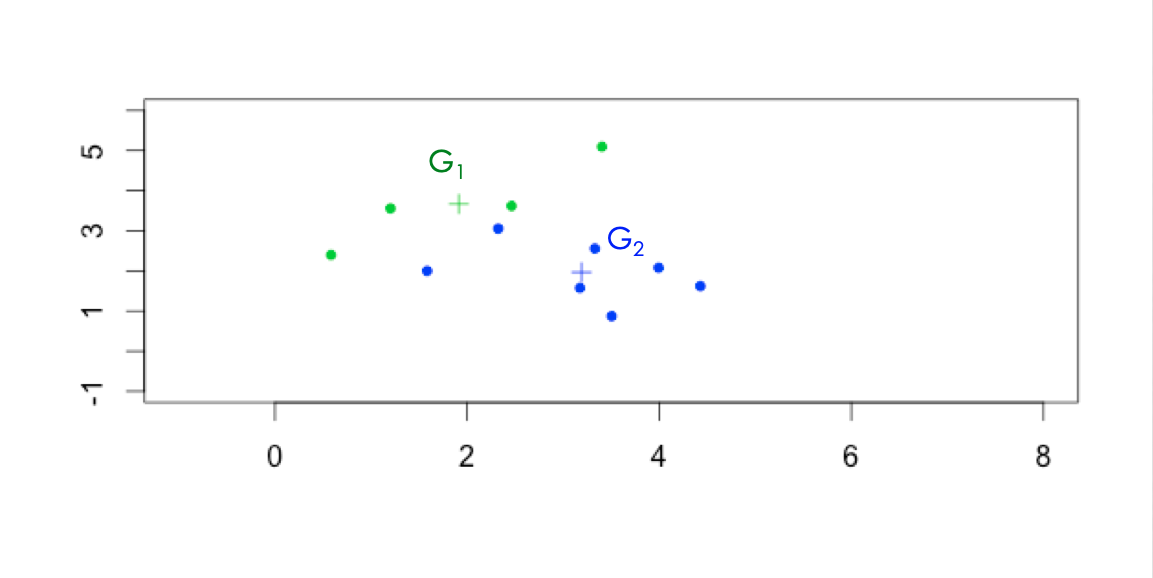
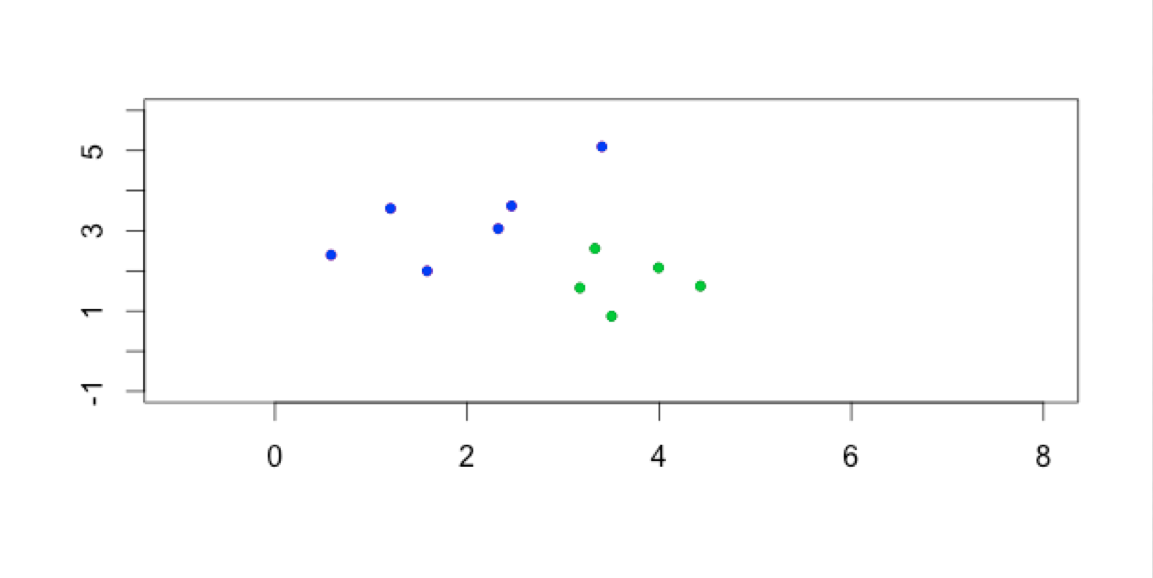
K-means clustering with 5 clusters of sizes 24, 9, 50, 49, 18
Cluster means:
Sepal.Length Sepal.Width Petal.Length Petal.Width
1 -0.4045571 -1.3455962 0.04031425 -0.03738991
2 1.9201365 -0.3099829 1.42110076 1.03583907
3 0.4186461 -0.3655555 0.60612988 0.55450771
4 -0.9987207 0.9032290 -1.29875725 -1.25214931
5 1.1351750 0.5057616 1.08750903 1.40026317
Clustering vector:
[1] 4 4 4 4 4 4 4 4 4 4 4 4 4 4 4 4 4 4 4 4 4 4 4 4 4 4 4 4 4 4 4 4 4 4 4 4 4 4 4 4 4 1 4 4 4 4 4 4 4 4 3 3 3 1 3 3 3 1 3 1 1 3 1 3 1 3 3 1 1 1 3 3 3 3 3 3 3 3 3 1 1 1 1 3 3 3 3 1 3 1 1 3 1 1 1 3 3 3 1 1 5 3 2 3 5 2 1 2 3 5 5 3 5 3 3 5 3 5 2 1 5 3 2 3 5 2 3 3 3 2 2 5 3 3 3 2 5 3 3 5 5 5 3 5 5 5 3
[148] 3 5 3
Within cluster sum of squares by cluster:
[1] 18.898041 3.091184 30.436677 40.121722 12.220084
(between_SS / total_SS = 82.4 %)
Available components:
[1] "cluster" "centers" "totss" "withinss" "tot.withinss" "betweenss" "size" "iter" "ifault" si les individus d’un même cluster sont proches
si les individus de 2 clusters différents sont éloignés => variance inter forte
La coupure de l’arbre à un niveau donné construit une partition. la coupure doit se faire :
après les agrégations correspondant à des valeurs peu élevées de l’indice
avant les agrégations correspondant à des niveaux élevés de l’indice, qui dissocient les groupes bien distincts dans la population.
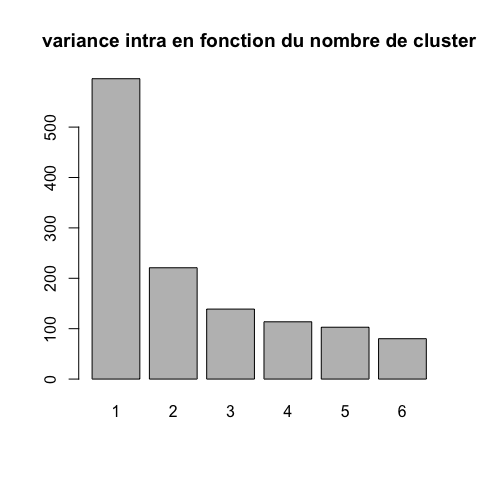
par une table
| k | 1 k | 2 k | 3 |
|---|---|---|---|
| c1 | 0 | 29 | 0 |
| c2 | 0 | 20 | 0 |
| c3 | 0 | 1 | 29 |
| c4 | 21 | 0 | 24 |
| c5 | 26 | 0 | 0 |
| Algorithme | Pros | Cons |
|---|---|---|
| Hiérarchique | L’arbre reflète la nature imbriquée de tous les sous-clusters | Complexité quadratique (mémoire et temps de calcul) \(\rightarrow\) quadruple chaque fois qu’on double le nombre d’individus |
| Permet une visualisation couplée dendrogramme (groupes) + heatmap (profils individuels) | ||
| Choix a posteriori du nombre de clusters | ||
| K-means | Rapide (linéaire en temps), peut traiter des jeux de données énormes (centaines de milliers de pics ChIP-seq) | Positions initiales des centres est aléatoire \(\rightarrow\) résultats changent d’une exécution à l’autre |
| Distance euclidienne (pas appropriée pour transcriptome par exemple) |
species.colors <- c(setosa = "#BB44DD", virginica = "#AA0044", versicolor = "#4400FF")
plot(mes.iris, col = species.colors[iris$Species], cex = 0.7)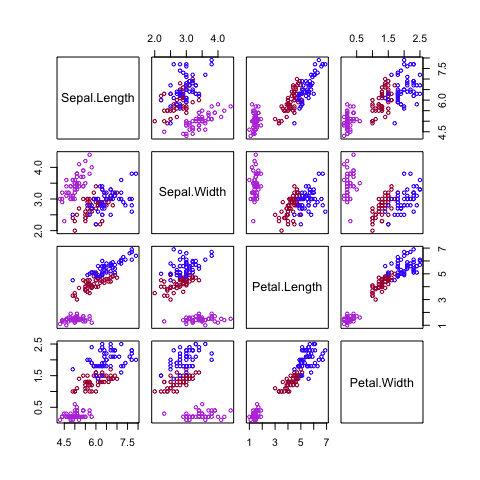
POUR ALLER PLUS LOIN
distance euclidienne ou distance \(L_2\): \(d(x,y)=\sqrt{\sum_i (x_i-y_i)^2}\)
distance de manahattan ou distance \(L_1\): \(d(x,y)=\sum_i |x_i-y_i|\)
distance du maximum ou L-infinis, \(L_\infty\): \(d(x,y)=\max_i |x_i-y_i|\)
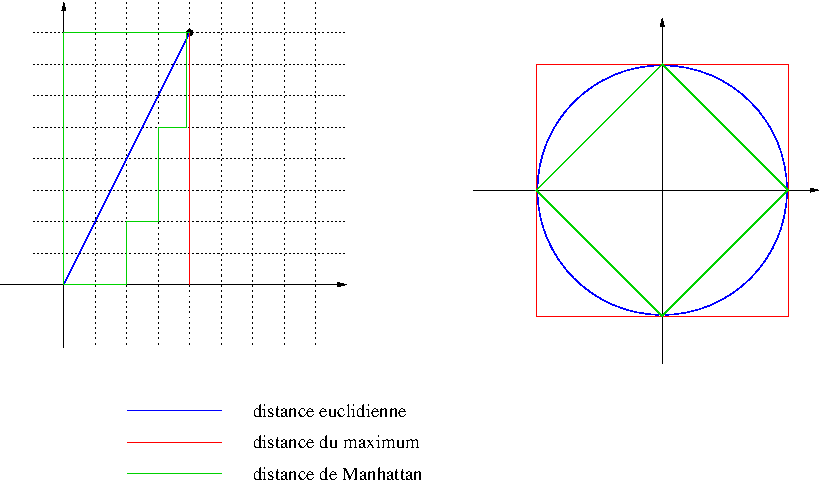
distance de Minkowski \(l_p\): \[d(x,y)=\sqrt[p]{\sum_i (|x_i-y_i|^p}\]
distance de Canberra (x et y valeurs positives): \[d(x,y)=\sum_i \frac{x_i-y_i}{x_i+y_i}\]
distance binaire ou distance de Jaccard ou Tanimoto: proportion de propriétés communes
Note : lors du TP, sur les données d’expression RNA-seq, nous utiliserons le coefficient de corrélation de Spearman et la distance dérivée, \(d_c = 1-r\)
Utilisées en bio-informatique:
Distance de Hamming: nombre de remplacements de caractères (substitutions)
Distance de Levenshtein: nombre de substitutions, insertions, deletions entre deux chaînes de caractères
\[d("BONJOUR", "BONSOIR")=2\]
Distance d’alignements: distances de Levenshtein avec poids (par ex. matrices BLOSSUM)
Distances d’arbre (Neighbor Joining)
Distances ultra-métriques (phylogénie UPGMA)
Il existe d’autres mesures de distances, plus ou moins adaptées à chaque problématique :
Jaccard (comparaison d’ensembles): \(J_D = \frac{A \cap B}{A \cup B}\)
Distance du \(\chi^2\) (comparaison de tableau d’effectifs)
Ne sont pas des distances, mais indices de dissimilarité :
Jensen-Shannon (comparaison de distributions) # Distance avec R : indice de Jaccard
ou pour des distances particulières, par exemple l’indice de Jaccard :
| v.a | 0 | 1 | 0 | 0 | 0 | 0 | 0 |
| v.b | 0 | 1 | 0 | 0 | 0 | 1 | 0 |
| v.c | 0 | 1 | 0 | 0 | 0 | 0 | 0 |
v.a v.b
v.b 0.3333333
v.c 0.0000000 0.3333333Mesure de similarité entre deux clustering
à partir du nombre de fois que les classifications sont d’accord
\[R=\frac{m+s}{t}\]
\[ \text{ARI} = \frac{\text{RI}-\text{E(RI)}}{\text{Max RI} - \text{E(RI)}}\]
[1] 0.4637776par(mfrow = c(1,2))
biplot(prcomp(mes.iris), las = 1, cex = 0.7,
main = "Données non normalisées")
biplot(prcomp(mes.iris, scale = TRUE), las = 1, cex = 0.7,
main = "Données normalisées")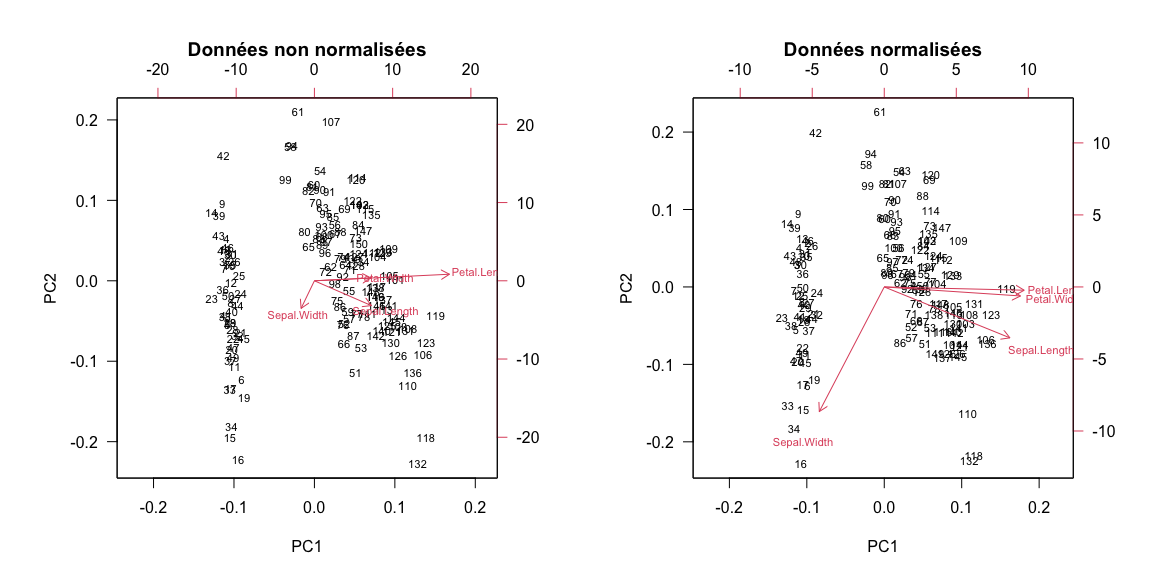
Contact: anne.badel@univ-paris-diderot.fr
Comment déterminer le nombre de clusters ? (1)
Ces méthodes non supervisées, sont sans a priori sur la structure, le nombre de groupe, des données.
rappel : un cluster est composé