Two main approches

• Gene set comparison or over-representation analysis (ORA)
  • Input: a set of functionally related genes
  • Reference: a database of annotated gene functions (GO, pathways, TF targets…)
  • Approach: evaluate the significance of the intersection (over-represented?)
  • Stat: hypergeometric test
• Gene Set Enrichment analysis
  • Input: a sorted list of genes
  • Reference: a database of annotated gene functions (GO, pathways, TF targets…)
  • Approach: evaluate the significance of the rank of the genes belonging to a reference class in the ordered list.
  • Stat: enrichment scores (alternative)

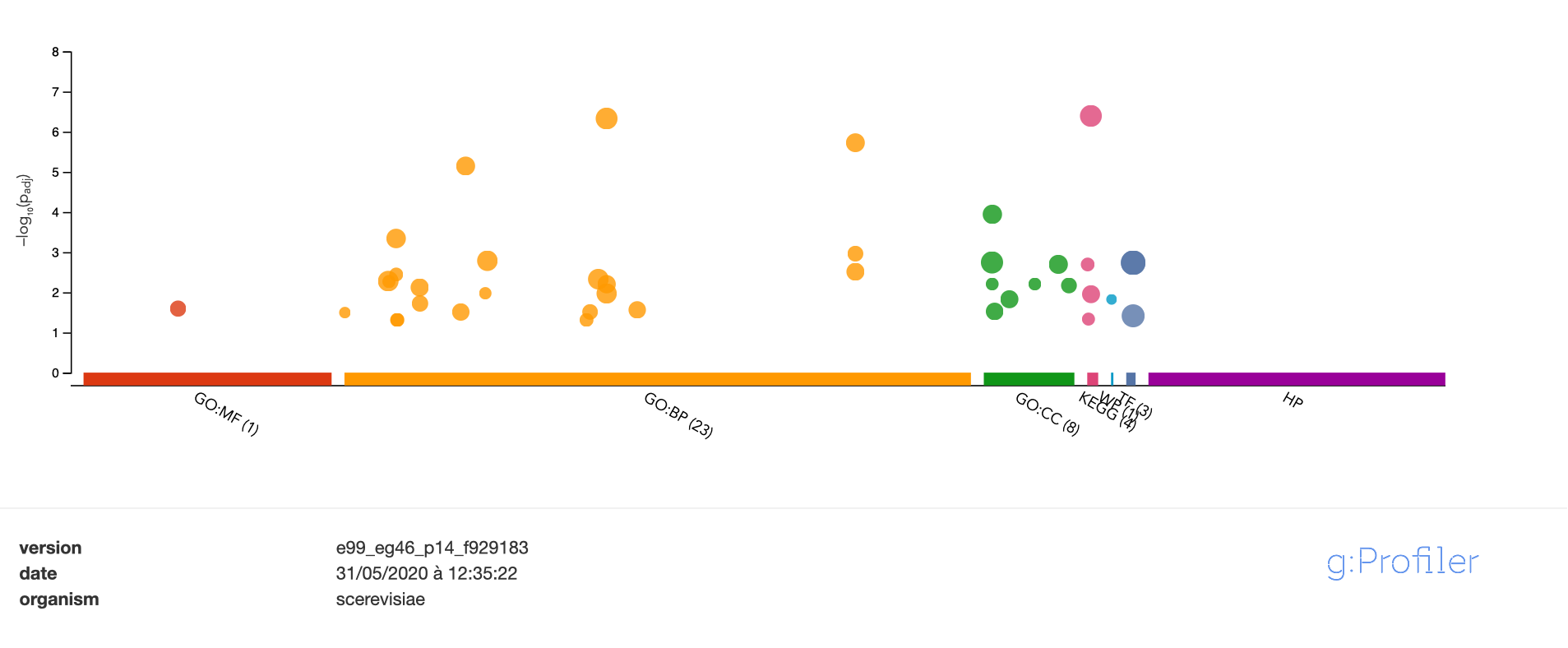
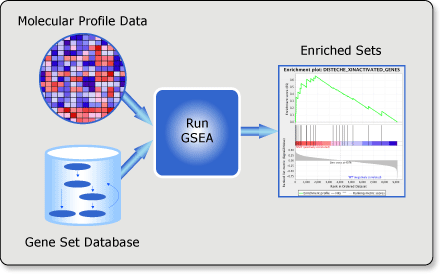
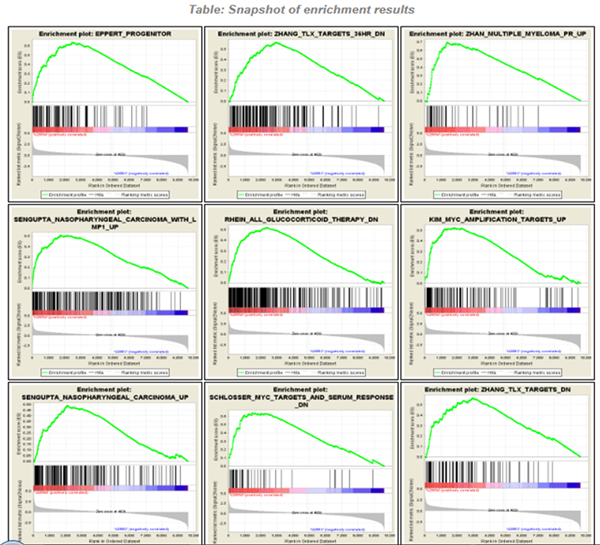
Gene set comparison (over-representation of the intersection)

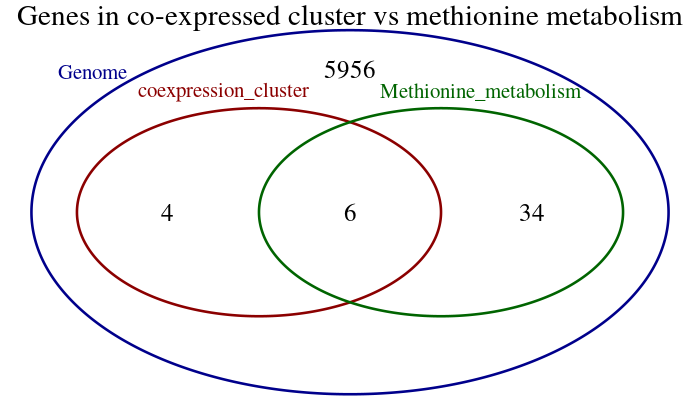
• A given organism has 6000 genes, 40 of which are involved in methionine metabolism.
• A set of 10 genes were reported as co-expressed in an RNAseq experiment. Among them, 6 are related to methionine metabolism.
• How significant is this observation ? More precisely, what would be the probability to observe such a correspondence by chance alone ?

The hypergeometric test

• We calculate the number of possibilities for the following selections

The hypergeometric test - probabilities

• Probability to have exactly 6 methionine genes within a selection of 10

  \[P(X=6) = \frac{C4}{C1} = \frac{C_{m}^{x}C_{n}^{k-x}}{C_{m+n}^{k}} = \frac{C_{40}^{6}C_{5960}^{4}}{C_{6000}^{10}} = 1.219e^{-11}\]

• Probability to have at least 6 methionine genes within a selection of 10

  \[P(X \ge 6) = \sum_{i=x}^{k}\frac{C_{m}^{i}C_{n}^{k-i}}{C_{m+n}^{k}} = 1.222e^{-11}\]

ORA - precautions to take

• Define your universe (background)
  • set with all the genes susceptible to be part of your analysis
• Not so simple
  • all genes in genomic annotations ?
  • all genes with at least one annotation in the ontology you used ?
  • all coding genes ?
  • genes on a biochip ?
  • genes / proteins detected by an experimental approach (RNAseq, proteomics)
  • genes reachable by your approach (ex : miRNA targets, Godard et al., 2015)
• Multiple-test corrections
  • correction choice (adjusted P-values : Bonferroni correction, Benjamini-Hochberg FDR…)
  • inter-test dependancies corrections (gSCS in gProfiler)

Practical - Annotating a group of differentially expressed genes (DEG)

• tool: g:GOSt from gProfiler https://biit.cs.ut.ee/gprofiler/gost
• documentation: https://biit.cs.ut.ee/gprofiler/page/docs
• Goal:
  • detect functions (biological process, pathways, regulation…) associated with the set of DEG
  • interpret the resuls
• What about a negative control ?

Practical - DEG

• Organism: Saccharomyces cerevisiae

• Data source: https://www.ncbi.nlm.nih.gov/geo/query/acc.cgi?acc=GSE89530

• The aim of this study is to compare NGS-derived yeast transcriptome profiling (RNA-seq) of wild-type and bdf1-Y187F-Y354F mutant strains after sporulation induction (time points: 0h 4h and 8h)

• design: S. cerevisiae wild-type and bdf1-Y187F-Y354F mutant strains were collected 0h, 4h and 8h after sporulation induction in triplicates. mRNA were purified, prepared and sequenced using Illumina HiSeq 2000 sequencer

• WT vs mutant at 0h: bdf1_Y187F_Y354F_mutant_0__vs__Wild_type_0_DESeq2_positive_geneIDs.txt

• WT vs mutant at 4h: bdf1_Y187F_Y354F_mutant_4__vs__Wild_type_4_DESeq2_positive_geneIDs.txt

Practical - Results

• t0:

Practical - Results

• t4:

Practical - detailled results t0

Practical - detailled results t4

gProfiler in R

• Package: https://cran.r-project.org/web/packages/gprofiler2/index.html
• Manual: https://cran.r-project.org/web/packages/gprofiler2/gprofiler2.pdf
• Vignettes: https://cran.r-project.org/web/packages/gprofiler2/vignettes/gprofiler2.html

Gene Set Enrichment Analysis

• GSEA
• Broad Institute
• since 2006
• determines whether an a priori defined set of genes shows statistically significant, concordant differences between two biological states
• http://software.broadinstitute.org/gsea/index.jsp
• MSigDB (The Molecular Signatures Database) : collection of annotated gene sets (https://www.gsea-msigdb.org/gsea/msigdb/index.jsp)
• R package : https://bioconductor.org/packages/release/bioc/html/GSEABase.html

GSEA principle

• All genes are sorted according to some criterion (e.g. differential expression p-value, correlation of expression with other variables, …).

• Each graph compares the ranked gene list with one reference class (e.g. one biological process).

• Black bars denote genes belonging to the reference class.

• The green curve estimates, at each level i, the degree of over-representation of the reference genes in the i top-ranking genes.