Basic data structures in R – matrices, data frames and lists

Exercice 1

Créez la matrice identité matIdentite de dimension 10 lignes x 10 colonnes contenant uniquement le chiffre 0. Puis remplacez uniquement les valeurs de la diagonale par le chiffre \(1\). Imprimez la matrice à l’écran.
Créez une matrice matAleatoire contenant des valeurs tirées aléatoirement de dimension 10 lignes x 10 colonnes, dont les éléments suivent une loi normale de moyenne 0 et de variance \(5\). Imprimez la matrice à l’écran en arrondissant à 2 décimales. Fonctions recommandées : matrix(), diag(), print(), rnorm(),round()`

Solutions

En cas d’urgence poussez sur Code pour révéler la solution.

matIdentite <- matrix(data = 0, ncol = 10, nrow = 10)
diag(matIdentite) <- 1 #diag() retourne un vecteur dont on peut remplacer les valeurs 0 par 1
print(matIdentite)

      [,1] [,2] [,3] [,4] [,5] [,6] [,7] [,8] [,9] [,10]
 [1,]    1    0    0    0    0    0    0    0    0     0
 [2,]    0    1    0    0    0    0    0    0    0     0
 [3,]    0    0    1    0    0    0    0    0    0     0
 [4,]    0    0    0    1    0    0    0    0    0     0
 [5,]    0    0    0    0    1    0    0    0    0     0
 [6,]    0    0    0    0    0    1    0    0    0     0
 [7,]    0    0    0    0    0    0    1    0    0     0
 [8,]    0    0    0    0    0    0    0    1    0     0
 [9,]    0    0    0    0    0    0    0    0    1     0
[10,]    0    0    0    0    0    0    0    0    0     1

cat("2 variantes plus efficaces pour creer la matrice : \n")

2 variantes plus efficaces pour creer la matrice :

cat("------variante 1:\n")

------variante 1:

diag(1,10,10)

      [,1] [,2] [,3] [,4] [,5] [,6] [,7] [,8] [,9] [,10]
 [1,]    1    0    0    0    0    0    0    0    0     0
 [2,]    0    1    0    0    0    0    0    0    0     0
 [3,]    0    0    1    0    0    0    0    0    0     0
 [4,]    0    0    0    1    0    0    0    0    0     0
 [5,]    0    0    0    0    1    0    0    0    0     0
 [6,]    0    0    0    0    0    1    0    0    0     0
 [7,]    0    0    0    0    0    0    1    0    0     0
 [8,]    0    0    0    0    0    0    0    1    0     0
 [9,]    0    0    0    0    0    0    0    0    1     0
[10,]    0    0    0    0    0    0    0    0    0     1

cat("------variante 2:\n")

------variante 2:

diag(10)# en fait, par defaut, si on n'utilise qu'un seul argument dans la fonction diag(), la commande retourne une matrice de 0 sauf pour la diagonale contenant des 1

      [,1] [,2] [,3] [,4] [,5] [,6] [,7] [,8] [,9] [,10]
 [1,]    1    0    0    0    0    0    0    0    0     0
 [2,]    0    1    0    0    0    0    0    0    0     0
 [3,]    0    0    1    0    0    0    0    0    0     0
 [4,]    0    0    0    1    0    0    0    0    0     0
 [5,]    0    0    0    0    1    0    0    0    0     0
 [6,]    0    0    0    0    0    1    0    0    0     0
 [7,]    0    0    0    0    0    0    1    0    0     0
 [8,]    0    0    0    0    0    0    0    1    0     0
 [9,]    0    0    0    0    0    0    0    0    1     0
[10,]    0    0    0    0    0    0    0    0    0     1

Matrice de nombres aléatoires

## Generate a 10x10 matrix with random normal numbers
matAleatoire <- matrix(
  nrow = 10, 
  ncol = 10, 
  data = rnorm(n = 100, 
               mean = 0, 
               sd = sqrt(5)))
# as long as you specify the arguments, you may change the order to pass the arguments to the function 

## Print the results rounded at 2 decimals
print(round(matAleatoire, digits = 2))

       [,1]  [,2]  [,3]  [,4]  [,5]  [,6]  [,7]  [,8]  [,9] [,10]
 [1,]  1.17 -0.69  1.49 -1.15 -0.74  0.09 -0.12 -0.73  3.15  1.62
 [2,] -0.14 -0.62  0.12  1.84  0.58 -5.61 -0.43  0.98 -3.09 -0.70
 [3,]  1.21 -0.90 -0.34 -0.10  0.75  3.40 -1.70 -1.45  3.90 -2.09
 [4,]  4.14 -5.63 -3.04  2.09 -0.31  2.27 -1.54 -3.57  2.90  1.32
 [5,] -2.06 -1.22 -3.48 -1.85  2.36 -1.97  3.29 -2.47 -2.67 -2.42
 [6,] -1.07  2.71  0.08 -3.76  1.57  2.26  2.25 -0.19  0.95 -1.82
 [7,] -3.69 -0.52  0.39 -1.61 -2.67  0.05  1.68  0.88 -3.16 -0.41
 [8,] -2.87  2.55  1.93  2.21 -4.12  0.31 -4.23 -4.08  0.34  1.33
 [9,]  2.43 -1.56 -0.20  1.39  3.31 -2.11 -1.72  0.68 -2.57  1.14
[10,]  4.04 -1.67 -3.39  2.12 -0.24  1.17  1.13  2.70 -1.11 -0.31

Exercice 2

Exercice 2.1

Créez deux vecteurs aléatoires nommés x1 et x2, contenant chacun \(n = 10.000\) valeurs aléatoires respectivement compatibles:

avec une loi normale centrée réduite pour x1;
avec une loi uniforme définie sur l’intervalle \([0, 10]\) pour x2.

Vérifiez la distribution empirique de ces échantillons en dessinant des histogrammes.

Vérifiez si les paramètres de vos échantillons aléatoires correspondent à vos attentes (et à leur espérance statistique).

Fonctions recommandées : rnorm(), runif(), cbind(), rbind(), dim(), mean(), var(), min(), max(), summary(), hist(), summary…

Solutions

n <- 10000 ## define vector sizes
x1 <- rnorm(n = n, mean = 0, sd = 1) ## normal random
x2 <- runif(n = n, min = 0, max = 10) ## uniform random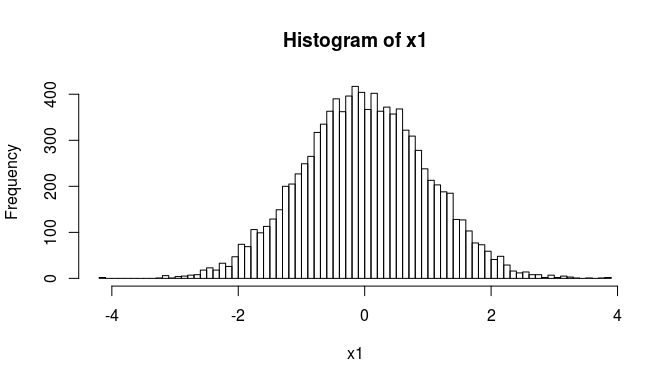

hist(x = x1, breaks = 100)

(too) simple istogram of normally distributed random numbers.

hist(x = x1, breaks = 100, 
     las = 1, 
     col = "palegreen",
     main = "Random normal numbers",
     xlab = "Value"
     )

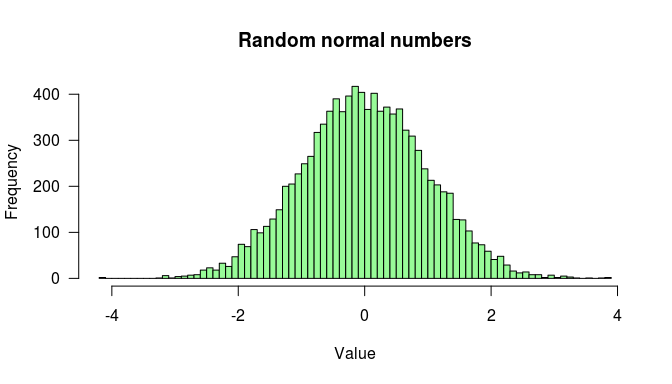
Histogram of normally distributed random numbers.

hist(x = x2, breaks = 10, 
     las = 1, 
     col = "cyan",
     main = "Uniformly distributed random numbers",
     xlab = "Value"
     )

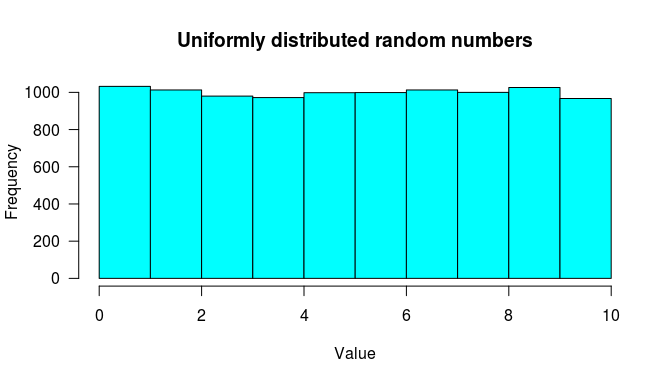
Histogram of uniformly distributed random numbers.

summary(x1)

     Min.   1st Qu.    Median      Mean   3rd Qu.      Max. 
-4.197330 -0.668833 -0.016913 -0.006186  0.663910  3.813476

Exercice 2.2

Créez une matrice m1 qui contient les 10 premières valeurs de x1 (colonne 1 de m1) et les 10 dernières valeurs de x2 (colonne 2 de m1). Verifiez qu’il s’agit bien d’une matrice et affichez ses dimensions.

Fonctions recommandées : matrix(), class(), dim(), cbind(),…

Solution

## Prepare an empty matrix
m1 <- matrix(nrow = 10, ncol = 2)

## Assign values to the first column
m1[, 1] <- head(x = x1, n = 10) ## equivalent to m1[, 1] <- x1[1:10]

## Assign values to the second column
m1[, 2] <- tail(x = x1, n = 10)

## Print the result rounded to 3 decimals
print(round(m1, digits = 3))

        [,1]   [,2]
 [1,]  0.854  0.400
 [2,]  1.822  1.081
 [3,]  1.706 -1.198
 [4,] -0.601 -0.302
 [5,]  0.323 -0.033
 [6,] -0.307  0.833
 [7,] -1.463 -0.002
 [8,]  0.860 -1.645
 [9,]  0.075  1.785
[10,] -1.355 -0.580

## Check it is a matrix and print its dimensions
class(m1)

[1] "matrix"

dim(m1)

[1] 10  2

## Alternatively and more quickly you may use the function cbind() to directly generate the matrix m1 in one command line
m1 <- cbind(x1[1:10], x2[91:100])
print(round(m1, digits = 3))

        [,1]  [,2]
 [1,]  0.854 5.205
 [2,]  1.822 0.938
 [3,]  1.706 2.792
 [4,] -0.601 1.177
 [5,]  0.323 1.612
 [6,] -0.307 5.782
 [7,] -1.463 3.122
 [8,]  0.860 2.120
 [9,]  0.075 4.631
[10,] -1.355 3.456

class(m1)

[1] "matrix"

dim(m1)

[1] 10  2

Exercice 2.3

Créez une matrice m2 qui contient

les 16ème, 51ème, 79ème, 31ème et 27ème valeurs de x1 (colonne 1 de m2) et
les 30ème, 70ème, 12ème, 49ème et 45ème de x2 (colonne 2 de m2).

Fonctions recommandées : matrix(), cbind(),…

Solutions

m2 <- matrix(nrow = 5, ncol = 2)

## Assign values
m2[, 1] <- x1[c(16, 51, 79, 31, 27)]
m2[, 2] <- x2[c(30, 70, 12, 49, 45)]

## Print the result
print(m2)

            [,1]      [,2]
[1,] -0.50025450 7.0688692
[2,]  0.74241398 0.8427670
[3,] -0.07371413 3.8186685
[4,]  0.16255732 0.7407108
[5,]  1.13301686 8.4405706

## or more directly using the cbind() function without creating an empty matrix first
m2 <- cbind(x1[c(16, 51, 79, 31, 27)], x2[c(30, 70, 12, 49, 45)])
print(m2)

            [,1]      [,2]
[1,] -0.50025450 7.0688692
[2,]  0.74241398 0.8427670
[3,] -0.07371413 3.8186685
[4,]  0.16255732 0.7407108
[5,]  1.13301686 8.4405706

Exercice 2.4

Concaténez à la suite (l’une en dessous-de l’autre) les matrices m1 et m2, afin d’obtenir une nouvelle matrice m3. Quelles sont les dimensions (nombre de lignes et de colonnes) de m3 ?

Fonctions recommandées : rbind(), cbind(), dim(), ncol(), nrow(), str()

Solutions

m3 <- rbind(m1, m2)
print(m3)

             [,1]      [,2]
 [1,]  0.85401104 5.2049493
 [2,]  1.82236001 0.9377936
 [3,]  1.70591885 2.7915833
 [4,] -0.60052053 1.1773477
 [5,]  0.32278438 1.6124148
 [6,] -0.30670307 5.7817377
 [7,] -1.46251209 3.1218612
 [8,]  0.86032918 2.1195933
 [9,]  0.07502485 4.6314595
[10,] -1.35545445 3.4559670
[11,] -0.50025450 7.0688692
[12,]  0.74241398 0.8427670
[13,] -0.07371413 3.8186685
[14,]  0.16255732 0.7407108
[15,]  1.13301686 8.4405706

dim(m3)

[1] 15  2

nrow(m3)

[1] 15

ncol(m3)

[1] 2

pour aller plus loin:

Les operateurs classiques (+, -, ) font des operations terme a terme si les deux matrices ont la meme taille, par exemple: m1 + rbind(m2,m2) alors que m1+m2 retourne une erreur Pour faire du calcul matriciel, on utilise un operateur specifique %*% pour multiplier. La premiere matrice a autant de lignes qu’il y a de colonnes dans la 2eme matrice. La matrice resultante a autant de lignes que la 1ere matrice et de colonnes que la 2eme matrice. Quelques exemples:*

m4 <- m1 %*% t(m2)# m1 avec la transposee de m2 qui a 2 lignes et 5 colonnes
dim(m4)

[1] 10  5

m5 <- m1 %*% t(m1)# m1 avec sa propre tranposee
dim(m5)

[1] 10 10

m6 <- t(m1) %*% m1 # ou l'inverse! Pas de commutativite sur ces calculs!
dim(m6)

[1] 2 2

Exercice 3

Fonctions recommandées :

-data(WorldPhones), - class(), - dim(), - rownames(), - colnames(), - str(), - sum(), - apply(), - names(), - max(), - min(), - which(), - which.max(), - which.min() - …

Exercice 3.1

Importez dans votre session R les données nommées WorldPhones (pré-existantes dans R). Affichez le contenu de la variable WorldPhones. Quelle est sa structure et sa classe ?

Exercice 3.2

Calculez le nombre total de numéros de téléphone attribués :

au cours des différentes années (vecteur nbrTelAn)
pour chaque continent (vecteur nbrTelCont)

Exercice 3.3

Quel est le continent qui a le plus / moins de numéros attribués ?

Exercice 3.4

Dans combien de continents y a-t-il plus de : 20.000, 50.000 et 200.000 numéros de téléphone attribués ?

Solutions exercice 3

data("WorldPhones")
print(WorldPhones)

     N.Amer Europe Asia S.Amer Oceania Africa Mid.Amer
1951  45939  21574 2876   1815    1646     89      555
1956  60423  29990 4708   2568    2366   1411      733
1957  64721  32510 5230   2695    2526   1546      773
1958  68484  35218 6662   2845    2691   1663      836
1959  71799  37598 6856   3000    2868   1769      911
1960  76036  40341 8220   3145    3054   1905     1008
1961  79831  43173 9053   3338    3224   2005     1076

class(WorldPhones)

[1] "matrix"

dim(WorldPhones)

[1] 7 7

rownames(WorldPhones)

[1] "1951" "1956" "1957" "1958" "1959" "1960" "1961"

colnames(WorldPhones)

[1] "N.Amer"   "Europe"   "Asia"     "S.Amer"   "Oceania"  "Africa"   "Mid.Amer"

# nombre d'appels pour le continent 1
sum(WorldPhones[,1])

[1] 467233

# nombre d'appels pour le continent 2
sum(WorldPhones[,2])

[1] 240404

# etc.

# pour aller plus rapidement :
# repetition de la commande sum() en ligne = marginal sums per year
nbrTelAn <- apply(WorldPhones, 1, sum)
print(nbrTelAn)

  1951   1956   1957   1958   1959   1960   1961 
 74494 102199 110001 118399 124801 133709 141700

# repetition de la commande sum() en colonne =  marginal sums per continent
nbrTelCont <- apply(WorldPhones, 2, sum)
print(nbrTelCont)

  N.Amer   Europe     Asia   S.Amer  Oceania   Africa Mid.Amer 
  467233   240404    43605    19406    18375    10388     5892

# continent avec le plus de numeros
names(nbrTelCont)[which(nbrTelCont == max(nbrTelCont))]

[1] "N.Amer"

# continent avec le moins de numeros
names(nbrTelCont)[which(nbrTelCont == min(nbrTelCont))]

[1] "Mid.Amer"

# ou plus simplement avec la commande which.max() ou which.min()
names(which.max(nbrTelCont))

[1] "N.Amer"

names(which.min(nbrTelCont))

[1] "Mid.Amer"

#

## Another way: with head and tail
tail(sort(nbrTelCont), n = 1)

N.Amer 
467233

head(sort(nbrTelCont), n = 1)

Mid.Amer 
    5892

sum(nbrTelCont > 20000)

[1] 3

sum(nbrTelCont > 50000)

[1] 2

sum(nbrTelCont > 200000)

[1] 2

Exercice 4

Téléchargez le fichier minitable1.txt. Il est également disponible dans /shared/projects/dubii2020/data/module3/seance1/
Ouvrez-le avec un éditeur de texte ou un calculateur pour identifier sa structure et les cases non remplies.
Importez le dans R dans un objet test.data et vérifiez sa structure et son contenu.
Comment les données manquantes ont-elles été lues ? Remplacez-les par NA si elles n’ont pas été lues comme une donnée manquante.
Déplacez la colonne 1 en dernière colonne.
Renommez les colonnes colA, colB, colC, colD, colE… dans le nouvel ordre obtenu.
Supprimez la deuxième ligne.
Ajoutez une colonne de valeurs numériques obtenues en divisant les valeurs de la colE par les valeurs de la colA.
Dans la colC, remplacez les valeurs toto par tata et vice-versa.
Dans la colC, remplacez les lettres \(t\) par des \(m\).
Triez le dataframe par ordre croissant de la colonne colE.
Convertissez la colonne colB en valeurs numériques.
Dans un vecteur sumcolA, calculer la somme de la colA.
Faites un sous-dataframe test.data2 contenant les lignes pour lesquelles les éléments de la colE sont inférieurs ou égaux à ceux de la colA.
Sauvegardez le data frame test.data2 en fichier texte avec des ; comme séparateurs de champs.

Fonctions recommandées dans l’ordre : read.table(), str(), is.na(), paste(), gsub(), order(), as.integer(), sum(), subset(), write.table()

Solutions exercice 4

test.data <- read.table("/shared/projects/dubii2020/data/module3/seance1/minitable1.txt",
                        sep = "\t",
                        header = T,
                        stringsAsFactors = F,
                        fill = T)
str(test.data)

'data.frame':   6 obs. of  5 variables:
 $ colonne1: int  3 2 7 10 2 1
 $ colonne2: num  2.2 7.3 NA 10.1 8.9 3.2
 $ colonne3: logi  TRUE TRUE FALSE TRUE TRUE FALSE
 $ colonne4: chr  "toto" "toto" "tata" "titi" ...
 $ colonne5: chr  "oui" "non" "" "oui" ...

test.data

  colonne1 colonne2 colonne3 colonne4 colonne5
1        3      2.2     TRUE     toto      oui
2        2      7.3     TRUE     toto      non
3        7       NA    FALSE     tata         
4       10     10.1     TRUE     titi      oui
5        2      8.9     TRUE     toto      oui
6        1      3.2    FALSE     tutu      non

is.na(test.data) # la case [3,5] n'est pas lue comme une donnee manquante -> cf. help de read.table() pour l'argument na.strings de la fonction read.table(): par defaut, seules les donnees "NA" d'un vecteur de caracteres sont considerees comme des donnees manquantes, alors que pour les logical, integer, numeric and complex fields les cases vides sont bien lues comme des donnees manquantes

     colonne1 colonne2 colonne3 colonne4 colonne5
[1,]    FALSE    FALSE    FALSE    FALSE    FALSE
[2,]    FALSE    FALSE    FALSE    FALSE    FALSE
[3,]    FALSE     TRUE    FALSE    FALSE    FALSE
[4,]    FALSE    FALSE    FALSE    FALSE    FALSE
[5,]    FALSE    FALSE    FALSE    FALSE    FALSE
[6,]    FALSE    FALSE    FALSE    FALSE    FALSE

 # pour lire la case [3,5] comme une donnee manquante, on aurait pu taper la commande:
#test.data <- read.table("test.txt",sep="\t", header=T, stringsAsFactors=F, fill=T, na.strings="")

test.data[3,5] <- NA

test.data <- test.data[,c(2:5,1)]
names(test.data) <- paste("col", LETTERS[1:5], sep ="")
test.data <- test.data[-2,]
test.data$EbyA <- test.data$colE/test.data$colA
test.data[which(test.data$colC == "toto"),3] <- "otot"
test.data[which(test.data$colC == "tata"),3] <- "toto"
test.data[which(test.data$colC == "otot"),3] <- "tata"
test.data$colC <- gsub("t","m",test.data$colC)

test.data <- test.data[order(test.data$colE),]
test.data$colB <- as.numeric(test.data$colB)
sumcolA <- sum(test.data$colA,na.rm = T)
test.data2 <- subset(test.data, colE <= colA) # ou test.data2 <- test.data[which(test.data$colE <= test.data$colA),]
write.table(test.data2,file = "test2.txt", sep = ";", col.names = T,quote = F)

Exercice 5

Sauvegardez dans une liste session1_list tous les objets créés pendant les exercices 1 à 4 en les mettant dans des sous-listes correspondant à chaque exercice que vous nommerez exo1, exo2, exo3 et exo4.

Fonctions recommandées : list(), names()

Solutions exercice 5:

ls()# check what is in your environment

 [1] "m1"           "m2"           "m3"           "m4"           "m5"           "m6"           "matAleatoire" "matIdentite"  "n"            "nbrTelAn"     "nbrTelCont"   "sumcolA"      "test.data"    "test.data2"   "WorldPhones"  "x1"           "x2"

session1_list <- list()
#stepwise for exo1:
exo1 <- list("matIdentite" = matIdentite, "matAleatoire" = matAleatoire)
session1_list[["exo1"]] <- exo1
# or in one command for exo2:
session1_list[["exo2"]] <- list("x1" = x1, "x2" = x2, "m1" = m1, "m2" = m2, "m3" = m3, "m4" = m4, "m5" = m5, "m6" = m6)
# you may also add elements to the list one by one, either or not giveing the name directly with different ways:
session1_list[["exo3"]] <- list("WorlPhones" = WorldPhones)
session1_list[[3]][["nbrTelAn"]] <- list(nbrTelAn)
session1_list[[3]][3] <- list(nbrTelCont)
names(session1_list[[3]])[3] <- "nbrTelCont"
# or all elements for exo4 and naming it after:
session1_list[[4]] <- list("test.data" = test.data, "sumcolA" = sumcolA, "test.data2" = test.data2)
names(session1_list)[4] <- "exo4"

Basic data structures in R – matrices, data frames and lists

DUBii – Statistics with R

Claire Vandiedonck & Jacques van Helden

2020-03-10

Exercice 1

Solutions

Matrice de nombres aléatoires

Exercice 2

Exercice 2.1

Solutions

Exercice 2.2

Solution

Exercice 2.3

Solutions

Exercice 2.4

Solutions

pour aller plus loin:

Exercice 3

Exercice 3.1

Exercice 3.2

Exercice 3.3

Exercice 3.4

Solutions exercice 3

Exercice 4

Solutions exercice 4

Exercice 5

Solutions exercice 5: