A first data analysis with R – descriptive statistics, statistical tests
DUBii – Statistics with R
Claire Vandiedonck & Jacques van Helden
2020-03-05
Objectifs
Ce tutoriel vous montre comment représenter et analyser des variables qualitatives et quantitatives, et effectuer les principaux tests statistiques.
Le jeu de données diabdata est extrait d’une cohorte de patients diabétiques de type 2 suivis par le Dr Louis Potier à l’hopital Bichat. Il comporte, entre autres, des informations morphométriques (taille, poids) et biologiques (lipides sériques). Il inclut 1732 patients.
Solutions
En cas d’urgence poussez sur Code pour révéler la solution.
1. Importation des données
Le fichier à importer s’appelle diabdata.txt. Il est présent dans le répertoire /shared/projects/dubii2020/data/module3/seance2/
Ouvrez-le d’abord dans un éditeur de texte pour voir comment il est structuré. Importez-le dans votre session R ouverte dans votre répertoire de travail. Attention à la décimale!
Fonctions : setwd(),read.table(), str(), head(), tail()
setwd("~")
info_samples <- read.table("/shared/projects/dubii2020/data/module3/seance2/diabdata.txt", header=TRUE, sep=";", dec = "," , stringsAsFactors = FALSE)Regardez la structure de l’objet importé pour vérifier son format. Il s’agit d’un dataframe. Affichez également les premières lignes puis les dernières lignes de ce dataframe.
'data.frame': 1732 obs. of 7 variables:
$ identifiant: int 1 3 6 11 13 15 16 19 22 23 ...
$ genre : chr "M" "M" "M" "F" ...
$ origine : chr "AFRIQUE" "AFRIQUE" "AFRIQUE" "AFRIQUE" ...
$ tabac : chr "NON" "NON" "OUI" "OUI" ...
$ poids : num 86 65.8 96 58 53.2 71 61 64 51 90 ...
$ taille : int 181 169 186 161 180 175 175 160 165 170 ...
$ TG : num 0.74 1.22 1.79 1.21 1.19 1.15 0.48 0.93 0.49 1.16 ... identifiant genre origine tabac poids taille TG
1 1 M AFRIQUE NON 86.0 181 0.74
2 3 M AFRIQUE NON 65.8 169 1.22
3 6 M AFRIQUE OUI 96.0 186 1.79
4 11 F AFRIQUE OUI 58.0 161 1.21
5 13 M AFRIQUE OUI 53.2 180 1.19
6 15 F AFRIQUE NON 71.0 175 1.15 identifiant genre origine tabac poids taille TG
1727 1748 F EUROPE NON 70.0 162 2.32
1728 1749 M EUROPE NON 54.9 169 0.97
1729 1750 F EUROPE NON 68.5 167 2.04
1730 1751 F EUROPE NON 50.9 150 0.71
1731 1752 M EUROPE EX +5 ANS 72.0 174 1.90
1732 1754 M EUROPE EX +5 ANS 55.2 153 1.092. Variables qualitatives
2.1 L’identifiant
Que pensez-vous de l’identifiant des sujets? S’agit-il d’une variable qualitative ou quantitative? Si nécessaire, transformez le type de données de cette variable ìdentifiant pour qu’il s’agisse d’une chaîne de caractères et vérifiez le résultat.
Fonctions : as.character(), str()
'data.frame': 1732 obs. of 7 variables:
$ identifiant: chr "1" "3" "6" "11" ...
$ genre : chr "M" "M" "M" "F" ...
$ origine : chr "AFRIQUE" "AFRIQUE" "AFRIQUE" "AFRIQUE" ...
$ tabac : chr "NON" "NON" "OUI" "OUI" ...
$ poids : num 86 65.8 96 58 53.2 71 61 64 51 90 ...
$ taille : int 181 169 186 161 180 175 175 160 165 170 ...
$ TG : num 0.74 1.22 1.79 1.21 1.19 1.15 0.48 0.93 0.49 1.16 ...2.2 Description des variables qualititatives
Quelles sont les valeurs possibles des variables qualitatives?
Fonctions : unique()
[1] "M" "F"[1] "AFRIQUE" "AMERIQUE DU NORD" "AMERIQUE LATINE" "ASIE" "EUROPE" [1] "NON" "OUI" "EX +5 ANS"Combien d’occurences observe-t-on pour chaque valeur de ces varaibles?
Fonctions : table()
F M
712 1020
EX +5 ANS NON OUI
299 997 436
AFRIQUE AMERIQUE DU NORD AMERIQUE LATINE ASIE EUROPE
657 3 23 78 971 Compte-tenu des effectifs moindres pour les sujets d’origine d’Amérique du Nord et d’Amérique latine, regroupez ces deux catégories en une seule que vous appellerez AMERIQUE
2.3 Représentation graphique des distributions des variables qualititatives
Il existe deux principales fonctions graphiques primaires pour représenter les données qualitatives:
Une première représentation est celle en camembert. Faites un camembert des données concernant la consommation de tabac, le genre et l’origine. Vous pouvez jouer sur la couleur, l’orientation et modifier l’affichage des valeurs, ajouter un titre.
Fonctions : pie(), table()
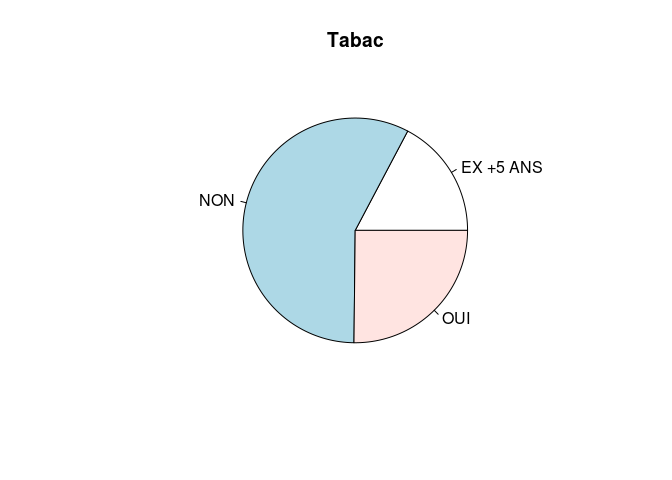
pie(table(info_samples$genre), col=c("pink", "blue"),
labels = c("Femmes", "Hommes"), main="Pie chart of the gender variable in the sample")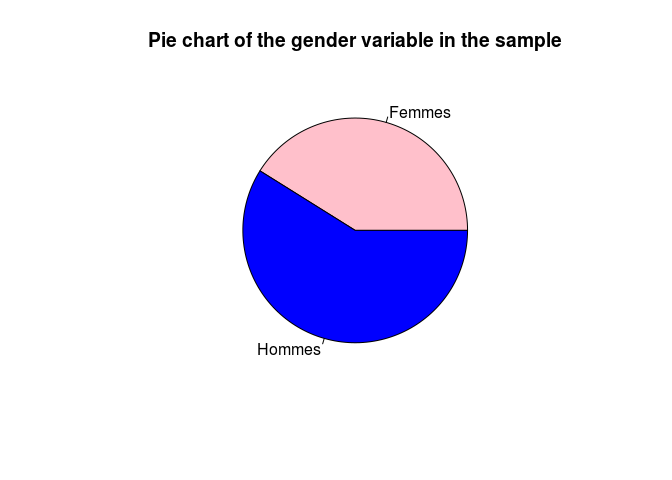
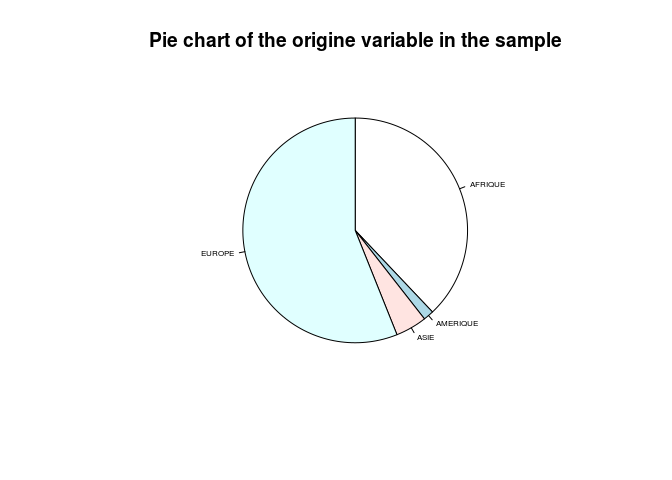
Ceendant, la représentation sous forme de camembert n’est pas recommandée car l’oeil a souvent du mal à comparer des aires différentes.
Une deuxième représentation qui est préférée pour celle des variables qualitatives est celle des diagrammes en bâtons. En ordonnées vous pouvez indiquer l’effectif ou la fréquence dans l’échantillon.
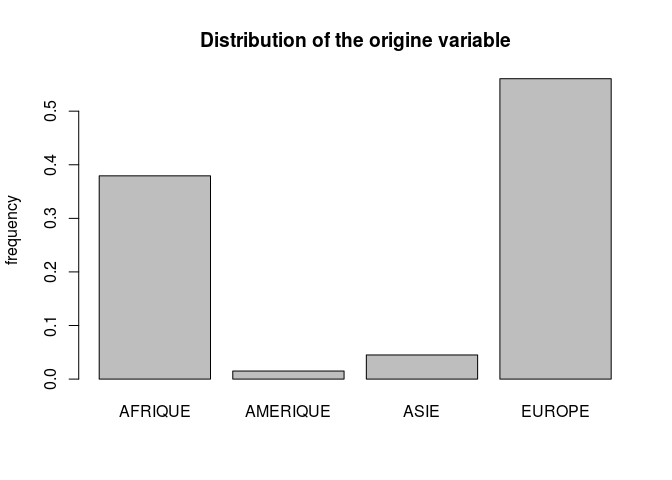
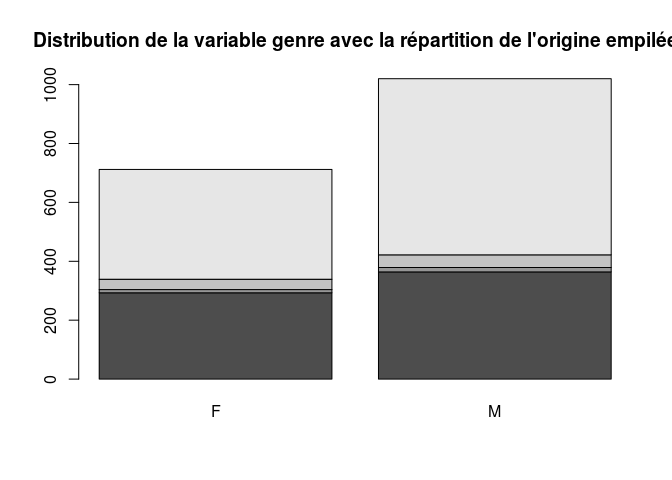
On peut également générer des tableaux de contingence de deux variables qualitatives et les représenter ensemble graphiquement dans des diagrammes en bâtons empilés.
AFRIQUE AMERIQUE ASIE EUROPE
F 293 11 35 373
M 364 15 43 598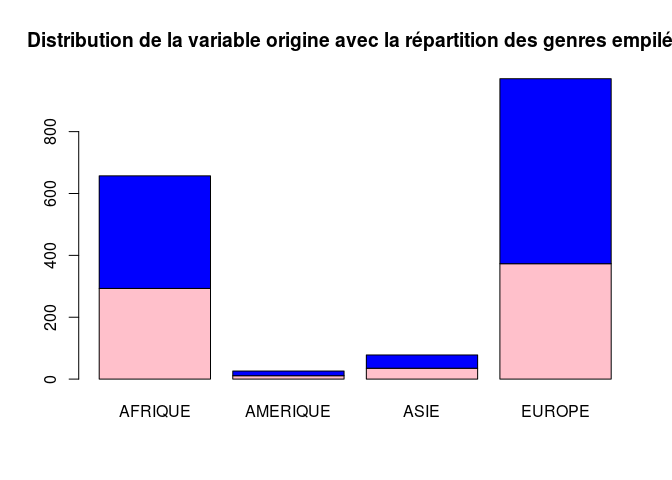
EX +5 ANS NON OUI
F 67 504 141
M 232 493 295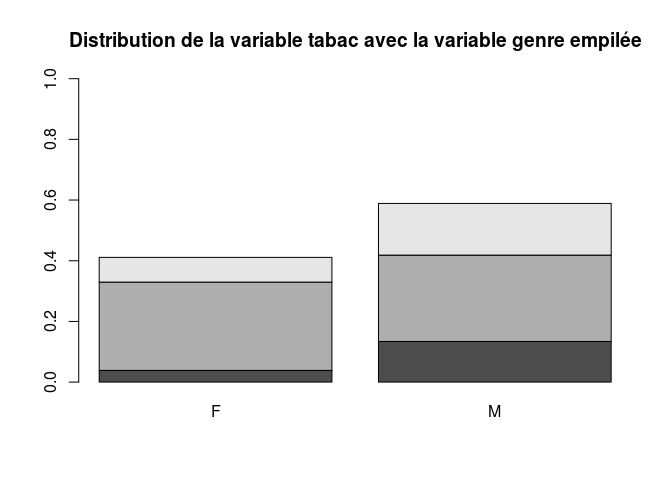
2.4 Tests statistiques sur variables qualitatives
On peut effectuer des tests de comparaison des proportions ou des distributions avec un test de Chi2 de Pearson.
Testez à présent si la distribution de la variable tabac est indépendante de celle du genre par un test de Chi2 à 2 degrés de libertés. L’hypothèse nulle est celle de distributions indépendantes, l’hypothèse alternative celle de variables liées. Extraire la p-value du test.
Pearson's Chi-squared test
data: info_samples$tabac and info_samples$genre
X-squared = 93.763, df = 2, p-value < 2.2e-16List of 9
$ statistic: Named num 93.8
..- attr(*, "names")= chr "X-squared"
$ parameter: Named int 2
..- attr(*, "names")= chr "df"
$ p.value : num 4.36e-21
$ method : chr "Pearson's Chi-squared test"
$ data.name: chr "info_samples$tabac and info_samples$genre"
$ observed : 'table' int [1:3, 1:2] 67 504 141 232 493 295
..- attr(*, "dimnames")=List of 2
.. ..$ info_samples$tabac: chr [1:3] "EX +5 ANS" "NON" "OUI"
.. ..$ info_samples$genre: chr [1:2] "F" "M"
$ expected : num [1:3, 1:2] 123 410 179 176 587 ...
..- attr(*, "dimnames")=List of 2
.. ..$ info_samples$tabac: chr [1:3] "EX +5 ANS" "NON" "OUI"
.. ..$ info_samples$genre: chr [1:2] "F" "M"
$ residuals: 'table' num [1:3, 1:2] -5.04 4.65 -2.86 4.21 -3.89 ...
..- attr(*, "dimnames")=List of 2
.. ..$ info_samples$tabac: chr [1:3] "EX +5 ANS" "NON" "OUI"
.. ..$ info_samples$genre: chr [1:2] "F" "M"
$ stdres : 'table' num [1:3, 1:2] -7.23 9.3 -4.3 7.23 -9.3 ...
..- attr(*, "dimnames")=List of 2
.. ..$ info_samples$tabac: chr [1:3] "EX +5 ANS" "NON" "OUI"
.. ..$ info_samples$genre: chr [1:2] "F" "M"
- attr(*, "class")= chr "htest"[1] 4.361162e-213. Variables quantitatives
3.1 Description des variables quantitatives
Le jeu de données comprend 3 variables quantitatives continues: la taille, le poids et le taux de triglycérides sériques TG
Définissez une nouvelle variable ìmc correspondant à l’indice de masse corporelle. On rappelle qu’il s’agit du poids en kg divisé par le carré de la taille en m². Arrondissez cette valeur à deux décimales.
3.2 Distribution des variables quantitatives
Affichez les valeurs de dispersion de ces variables.
poids taille TG imc
Min. : 36.80 Min. :138.0 Min. : 0.099 Min. :14.02
1st Qu.: 68.50 1st Qu.:162.0 1st Qu.: 0.960 1st Qu.:24.17
Median : 81.00 Median :169.0 Median : 1.350 Median :28.36
Mean : 82.80 Mean :168.9 Mean : 1.746 Mean :29.06
3rd Qu.: 94.83 3rd Qu.:175.0 3rd Qu.: 1.990 3rd Qu.:32.91
Max. :171.00 Max. :200.0 Max. :96.000 Max. :56.93 Il existe plusieurs représentations possibles de ces distributions:
un histogramme auquel vous pouvez superposer la courbe de densité si vous avez affiché l’axe des ordonnées en fréquences plutôt qu’en effectifs.
une boîte à moustaches
des nuages de points à une dimension (
stripcharts)
Dessinez un histogramme pour chacune des variables taille et poids.
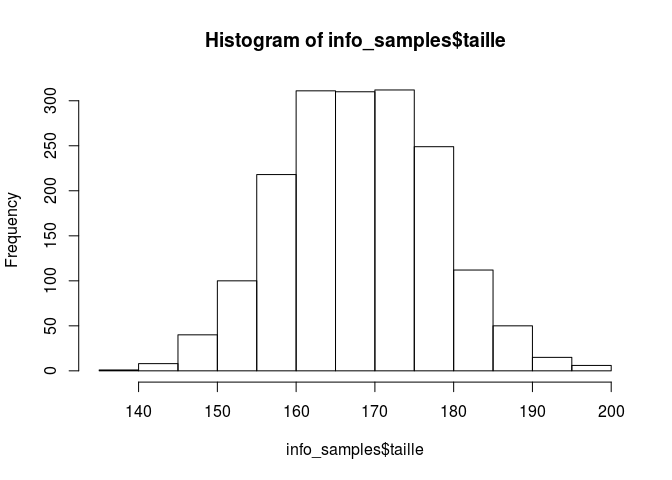
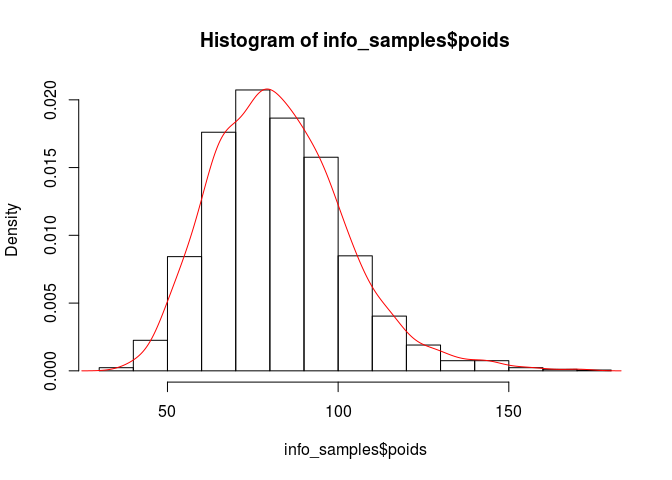
Dessinez ensuite dans une même fenêtre graphique côte à côte les boxplots des variables tailles et poids.
opar <- par() # pour sauvegardez les paramètres graphiques
par(mfrow=c(1,2)) # pour dessiner les deux boxplots sur une ligne et deux colonnes de la fenêtre graphique
boxplot(info_samples$taille, main="taille")
boxplot(info_samples$poids, main="poids")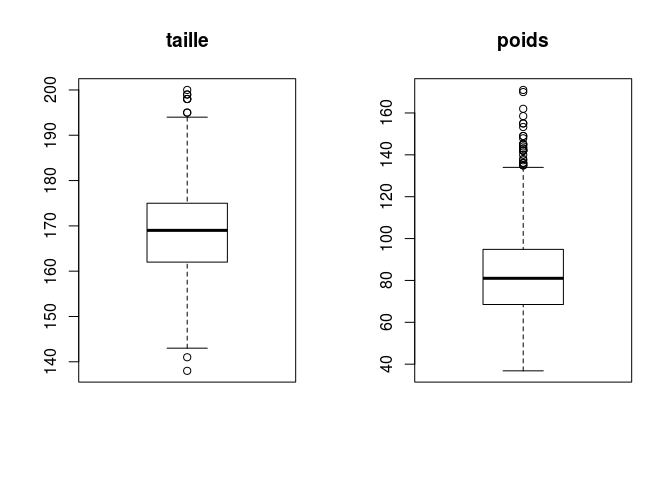
Dans une même fenêtre graphique, dessinez à présent l’un en dessous de l’autre un stripchart horizontal, un histogramme et un boxplot horizontal de la variable poids
opar <- par()
par(mfrow=c(3,1))
stripchart(info_samples$poids, vertical = F, axes=F, main="Distribution du poids")
hist(info_samples$poids, freq=F, xlab="", main="")
boxplot(info_samples$poids, horizontal = T, frame.plot=F, xlab="Poids")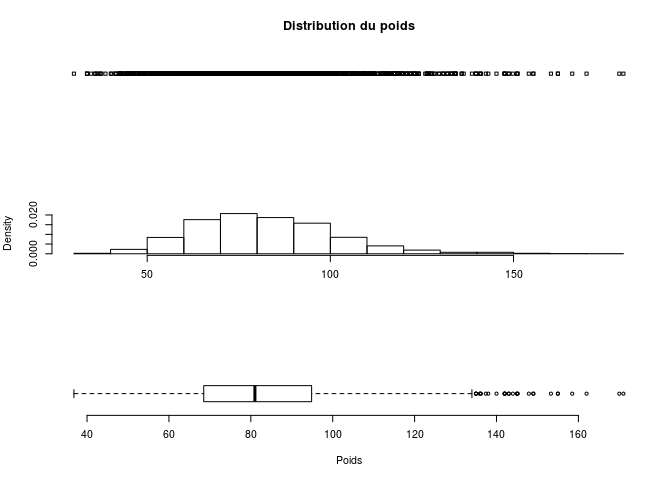
Quelle est l’influence des variables qualitatives sur ces distributions?
Nous allons explorer l’impact du facteur origine et de celui du genre sur la taille et le poids. Une première analyse exploratoire consiste à représenter ces distributions selon le facteur considéré.
Dessinez 4 boxplots de ces distributions dans une même fenêtre graphique.
opar <- par()
par(mfrow=c(2,2))
boxplot (info_samples$taille ~ info_samples$origine, xlab="Region", ylab="taille", col = "steelblue3")
boxplot (info_samples$poids ~ info_samples$origine, xlab="Region", ylab="poids", col = "steelblue3")
boxplot(info_samples$taille ~ info_samples$genre, xlab="Genre", ylab="taille", col = "steelblue3")
boxplot(info_samples$poids ~ info_samples$genre, xlab="Genre", ylab="poids", col = "steelblue3")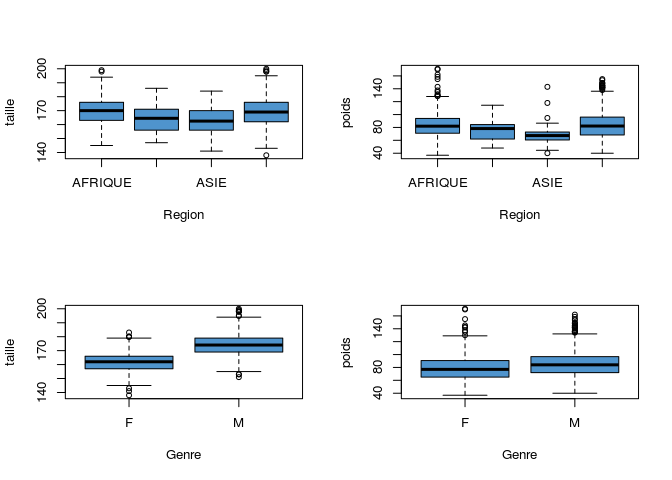
3.3 Tests statistiques sur des variables quantitatives
3.3.1 Tests de comparaison de 2 moyennes
Après avoir regardé les boxplots ci-dessus, on souhaite tester si le genre a effectivement un impact sur les variables taille et poids
Une première étape est de calculer les moyennes dans ces échantillons pour estimer les moyennes dans la population.
Commençons par la variable poids:
info_samples$genre: F
[1] 78.68933
---------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------
info_samples$genre: M
[1] 85.66723Les valeurs entre les échantillons sont différentes: m1≠m2 Cela ne signifie pas que μ1≠μ2
On doit réaliser un test statistique de comparaison de moyennes.
On teste d’abord l’homoscédasticité, cad l’égalité des variances dans les deux groupes.
info_samples$genre: F
[1] 364.0523
---------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------
info_samples$genre: M
[1] 375.7704
F test to compare two variances
data: info_samples$poids[info_samples$genre == "F"] and info_samples$poids[info_samples$genre == "M"]
F = 0.96882, num df = 711, denom df = 1019, p-value = 0.65
alternative hypothesis: true ratio of variances is not equal to 1
95 percent confidence interval:
0.8467144 1.1103638
sample estimates:
ratio of variances
0.9688158 Le test de comparaison des variances ne permet pas de rejeter l’hypothèse nulle de leur égalité.
Nous pouvons donc réaliser un test de Student.
Two Sample t-test
data: info_samples$poids by info_samples$genre
t = -7.4187, df = 1730, p-value = 1.844e-13
alternative hypothesis: true difference in means is not equal to 0
95 percent confidence interval:
-8.822686 -5.133113
sample estimates:
mean in group F mean in group M
78.68933 85.66723 Comparez à présent les moyennes et les variances de la variable taille en fonction du genre:
info_samples$genre: F
[1] 161.6236
---------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------
info_samples$genre: M
[1] 173.9716info_samples$genre: F
[1] 49.37992
---------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------
info_samples$genre: M
[1] 59.53305
F test to compare two variances
data: info_samples$taille[info_samples$genre == "F"] and info_samples$taille[info_samples$genre == "M"]
F = 0.82945, num df = 711, denom df = 1019, p-value = 0.007272
alternative hypothesis: true ratio of variances is not equal to 1
95 percent confidence interval:
0.7249166 0.9506406
sample estimates:
ratio of variances
0.8294539 ## l'égalité des variances ne peut être rejetée. On conduit donc un test de Welsh qui est proposé par défaut dans R avec la fonction t.test()
t.test(info_samples$taille ~ info_samples$genre) # le test est significatif avec une p-value < 2.2e-16
Welch Two Sample t-test
data: info_samples$taille by info_samples$genre
t = -34.552, df = 1613.8, p-value < 2.2e-16
alternative hypothesis: true difference in means is not equal to 0
95 percent confidence interval:
-13.04895 -11.64700
sample estimates:
mean in group F mean in group M
161.6236 173.9716 [1] 2.723553e-1963.3.2 Tests de comparaison de plus de 2 moyennes
Générons une nouvelle variable aléatoire en discrétisant la variable imc pour définir la variable ìmc_cat indiquant si les sujets sont maigres (imc < 18.5), de corpulence normale (entre 18.5 et 25), en surpoids (entre 25 et 30) ou obèses (au delà de 30). Transformez cette variable en facteur à 4 niveaux en attribuant le niveau 1 à une corpulence normale.
info_samples$imc_cat <- NA
info_samples$imc_cat[info_samples$imc<18.5] <- "maigreur"
info_samples$imc_cat[info_samples$imc>=18.5 & info_samples$imc<25] <- "normal"
info_samples$imc_cat[info_samples$imc>=25 & info_samples$imc<30] <- "surpoids"
info_samples$imc_cat[info_samples$imc>=30] <- "obesite"
info_samples$imc_cat <- factor(info_samples$imc_cat, levels=c("normal", "maigreur", "surpoids", "obesite"))Testons à présent si le poids moyen est bien différent entre ces 4 niveaux d’imc_cat. On procède d’abord à la vérification de l’homoscédasticité.
info_samples$imc_cat: normal
[1] 65.2202
---------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------
info_samples$imc_cat: maigreur
[1] 50.13077
---------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------
info_samples$imc_cat: surpoids
[1] 80.23193
---------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------
info_samples$imc_cat: obesite
[1] 99.00958info_samples$imc_cat: normal
[1] 77.90714
---------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------
info_samples$imc_cat: maigreur
[1] 45.00692
---------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------
info_samples$imc_cat: surpoids
[1] 105.3408
---------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------
info_samples$imc_cat: obesite
[1] 276.1399
Bartlett test of homogeneity of variances
data: poids by imc_cat
Bartlett's K-squared = 283.58, df = 3, p-value < 2.2e-16Les variances diffèrent significativement entre les groupes. On ne peut pas effectuer une analyse paramétrique (ANOVA). On effectue donc un test non paramétrique de Kruskal-Wallis:
Kruskal-Wallis rank sum test
data: log(info_samples$TG) by info_samples$imc_cat
Kruskal-Wallis chi-squared = 92.929, df = 3, p-value < 2.2e-163.3.3 Tests de corrélation entre deux variables continues
Les variables taille et poids sont-elles corrélées ?
Pearson's product-moment correlation
data: info_samples$taille and info_samples$poids
t = 13.809, df = 1730, p-value < 2.2e-16
alternative hypothesis: true correlation is not equal to 0
95 percent confidence interval:
0.2720314 0.3568991
sample estimates:
cor
0.315095 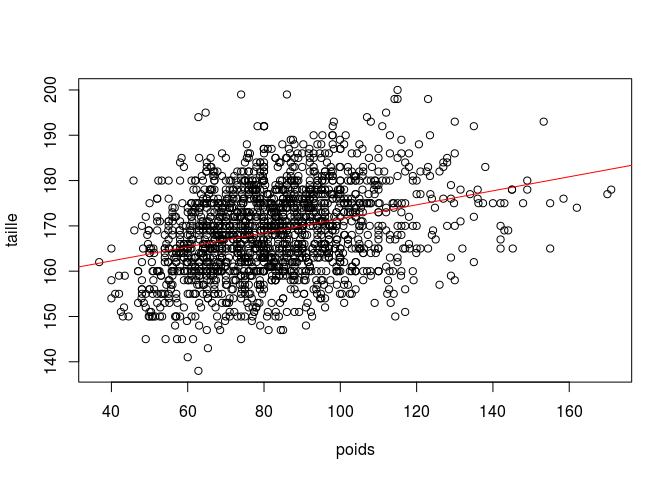
Les variables poids et imc sont-elles corrélées ?
Pearson's product-moment correlation
data: info_samples$poids and info_samples$imc
t = 75.488, df = 1730, p-value < 2.2e-16
alternative hypothesis: true correlation is not equal to 0
95 percent confidence interval:
0.8644082 0.8863841
sample estimates:
cor
0.8758494 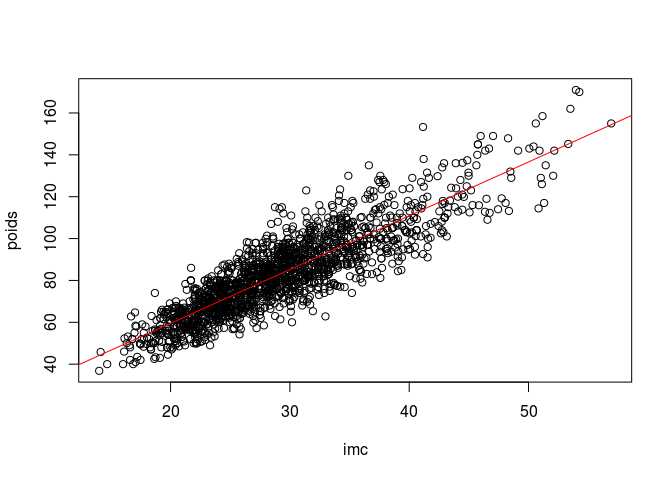
Le taux de triglycérides après transformation logarithmique est-il également corrélé à l’IMC?
Pearson's product-moment correlation
data: log(info_samples$TG) and info_samples$imc
t = 9.8042, df = 1730, p-value < 2.2e-16
alternative hypothesis: true correlation is not equal to 0
95 percent confidence interval:
0.1843193 0.2735730
sample estimates:
cor
0.2294284 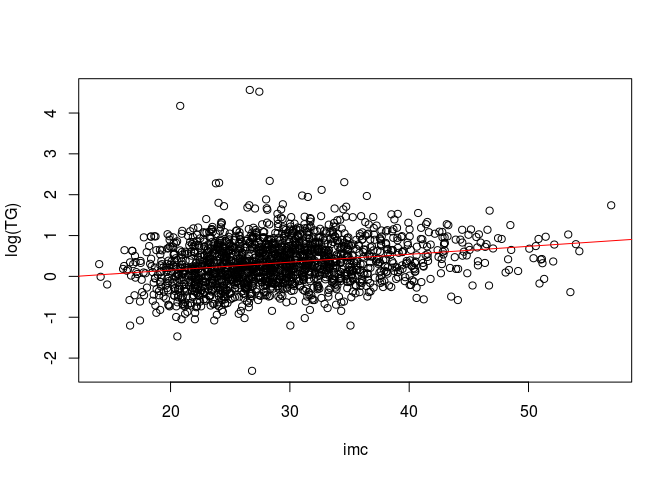
Il y a donc aussi une corrélation positive significative, bien que plus modeste en amplitude.
3.3.4 Tests de régression linéaire entre deux variables
Testons à présent l’impact des modalités d’imc (variable explicative) sur le taux de triglycérides en log (variable expliquée):
Call:
lm(formula = log(info_samples$TG) ~ info_samples$imc_cat)
Residuals:
Min 1Q Median 3Q Max
-2.6477 -0.3707 -0.0316 0.3547 4.2293
Coefficients:
Estimate Std. Error t value Pr(>|t|)
(Intercept) 0.16223 0.02487 6.522 9.09e-11 ***
info_samples$imc_catmaigreur -0.02523 0.09161 -0.275 0.783
info_samples$imc_catsurpoids 0.17283 0.03480 4.967 7.48e-07 ***
info_samples$imc_catobesite 0.29467 0.03252 9.061 < 2e-16 ***
---
Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
Residual standard error: 0.5506 on 1728 degrees of freedom
Multiple R-squared: 0.04795, Adjusted R-squared: 0.0463
F-statistic: 29.01 on 3 and 1728 DF, p-value: < 2.2e-16On constate un impact significatif du surpoids et de l’obésité sur ce taux de triglycérides!